题目内容
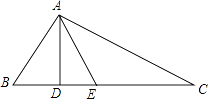
【题目】如图,将长方形ABC沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E. 
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求AE.
【答案】
(1)解:△BDE是等腰三角形,理由是:
由折叠得:∠EBD=∠DBC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴BE=DE,
∴△BDE是等腰三角形;
(2)解:设AE=x,则BE=DE=8﹣x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴AB2+AE2=BE2,
∴42+x2=(8﹣x)2,
x=3,
∴AE=3.
【解析】(1)由折叠和平行线性质可得:∠ADB=∠EBD,根据等角对等边得BE=DE,所以△BDE是等腰三角形;(2)设AE=x,则BE=DE=8﹣x,根据勾股定理列方程可求得AE的长.
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
时刻 | 9:00 | 9:45 | 12:00 |
碑上的数 | 是一个两位数,数字之和是9 | 十位与个位数字与9:00时所看到的正好相反 | 比9:00时看到的两位数中间多了个0 |
则小明在9:00时看到的两位数是____.