题目内容
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=3,点D是BC边上一动点(不与B,C重合),过点D做DE⊥BC交AB于点E,将∠B沿着直线DE翻折,点B落在BC边上的点F处,若∠AFE=90°,则BD的长是_____.
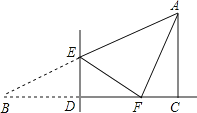
【答案】1.
【解析】
首先由在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,即可求得AC的长、∠AEF与∠BAC的度数,又由折叠的性质与三角函数的知识,即可求得CF的长,继而求得答案.
根据题意得:∠EFB=∠B=30°,DF=BD,EF=EB,
∵DE⊥BC,
∴∠FED=90°﹣∠EFD=60°,∠BEF=2∠FED=120°,
∴∠AEF=180°﹣∠BEF=60°,
∵在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,
∴AC=BCtan∠B=3×![]() ,∠BAC=60°,
,∠BAC=60°,
∵∠AFE=90°,
∵在Rt△ABC中,∠ACB=90°,
∴∠EFD+∠AFC=∠FAC+∠AFC=90°,
∴∠FAC=∠EFD=30°,
∴CF=ACtan∠FAC=![]() =1,
=1,
∴BD=DF=![]() =1;
=1;
故答案为:1.

练习册系列答案
相关题目