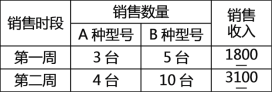题目内容
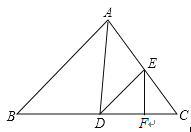
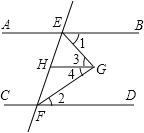
【题目】完成下面的证明：已知，如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD,求证：∠EGF＝90°
证明：∵HG∥AB（已知）
∴∠1＝∠3
又∵HG∥CD（已知）
∴∠2＝∠4
∵AB∥CD（已知）
∴∠BEF+ ＝180°
又∵EG平分∠BEF（已知）
∴∠1＝
∠
又∵FG平分∠EFD（已知）
∴∠2＝∠
∴∠1+∠2＝（ ）
∴∠1+∠2＝90°
∴∠3+∠4＝90° 即∠EGF＝90°．
【答案】两直线平行、内错角相等，∠EFD，两直线平行、同旁内角互补，∠BEF，∠EFD，∠BEF+∠EFD，等量代换
【解析】
此题首先由平行线的性质得出∠1＝∠3，∠2＝∠4，∠BEF+∠EFD＝180°，再由EG平分∠BEF，FG平分∠EFD得出∠1+∠2＝90°，然后通过等量代换证出∠EGF＝90°．
解：∵HG∥AB（已知）
∴∠1＝∠3 （两直线平行、内错角相等）
又∵HG∥CD（已知）
∴∠2＝∠4
∵AB∥CD（已知）
∴∠BEF+∠EFD＝180°（两直线平行、同旁内角互补）
又∵EG平分∠BEF（已知）
∴∠1＝
∠BEF，
又∵FG平分∠EFD（已知）
∴∠2＝∠EFD，
∴∠1+∠2＝（∠BEF+∠EFD），
∴∠1+∠2＝90°
∴∠3+∠4＝90° （等量代换），
即∠EGF＝90°．
故答案分别为：两直线平行、内错角相等，∠EFD，两直线平行、同旁内角互补，∠BEF，∠EFD，∠BEF+∠EFD，等量代换．
练习册系列答案
相关题目
【题目】某商场用2700元购进甲、乙两种商品共100件，这两种商品的进价、标价如下表所示：
| 甲种 | 乙种 |
进价（元/件） | 15 | 35 |
标价（元/件） | 20 | 45 |
（1）求购进两种商品各多少件？
（2）商品将两种商品全部卖出后，获得的利润是多少元？
