Question

【题目】如图，在四边形ABCD中，AB＝BC＝1，CD＝，DA＝1，且∠B＝90°．求：

（1）∠DAC的度数；

（2）四边形ABCD的面积（结果保留根号）；

（3）将△ABC沿AC翻折至△AB′C，如图所示，连接B′D，求△AB′D的面积．

Answer 1

【答案】（1）∠DAC=90°；（2）；（3）．

【解析】

（1）由于AB=BC=1，且∠B=90°根据勾股定理即可求出AC的长度，而CD=，DA=1，利用勾股定理的逆定理即可证明△ACD是直角三角形，由此即可求出∠DAC的度数；
（2）首先把求四边形ABCD的面积分割为求△ABC和△ACD的面积，然后利用三角形的面积公式可以分别求出这两个三角形的面积，最后就可以求出四边形ABCD的面积；

（3）作出△AB′D的边AB′边上的高DE，证明△ADE为等腰直角三角形，从而利用勾股定理可求出DE的长，进一步可得出△AB′D的面积．

解：（1）∵AB＝BC＝1，∠B＝90°，

∴∠BAC＝∠ACB＝45°，AC＝＝．

又∵CD＝，DA＝1，

∴AC2＋DA2＝CD2．

∴△ADC为直角三角形，∠DAC＝90°．

（2）∵S△ABC＝AB·BC＝，

S△ADC＝AD·AC＝，

∴S四边形ABCD＝S△ABC＋S△ADC＝．

（3）过点D作DE⊥AB′，垂足为E，

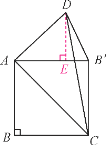
由（1）知∠DAC＝90°．

根据折叠可知∠B′AC＝∠BAC＝45°，AB＝AB′＝1，S△AB′C＝S△ABC＝．

∴∠DAE＝∠DAC－∠B′AC＝45°，∴∠DAE=∠AED=45°，

∴AE＝DE．

在Rt△ADE中，AE2＋DE2＝AD2，

∴2DE2＝1．∴DE＝．

∴S△ADB′＝×AB′×DE=×1×＝．