题目内容
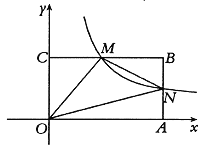
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16cm,DC=12cm,AD=21cm,点P以2cm/s的速度沿DA边由点D向点A运动,同时点Q以1cm/s的速度沿CB边由点C向点B运动,而且当其中一点停止运动时另一点也停止运动。设运功时间为t(s)
(1)用含t的代数式表示下面线段的长度:
①CQ=__________cm ; ②PD=__________cm
③BQ=__________cm ; ④AP=___________cm
(2)当t为_______s时,PQ∥AB
(3)是否存在某一时刻t,使得PQ⊥BD?若存在,求出t值;若不存在,请说明理由。

【答案】(1)t ; 2t ;(16-t); (21-2t);(2)5;(3)存在t,使得PQ⊥BD,t=9.
【解析】
(1)根据题意与图即可得出结论;
(2)根据PQ∥AB可得BQ=AP,再根据题意即可得出结论;
(3)根据题意可证出△BOQ∽△BCD ,△DOP∽△BCD,再根据相似三角形的性质即可分别得BO与DO,再根据BO+DO=20,即可得出结果.
(1)t ; 2t ;(16-t); (21-2t)
(2)5
(3)存在t,使得PQ⊥BD
解:∵BC=16cm,CD=12cm,∠C=90°
∴BD=20cm
设PQ与BD交于点O
当PQ⊥BD时,△BOQ∽△BCD ,△DOP∽△BCD
∴![]() ,解得
,解得![]()
同理可得![]()
∵B0+DO=20
∴![]() ,解得t=9
,解得t=9

练习册系列答案
相关题目