题目内容
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F. 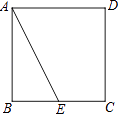
(1)画出旋转后的三角形.
(2)在(1)的条件下,
①求EF的长;
②求点E经过的路径弧EF的长.
【答案】
(1)解:如图1所示.△ADF为所求
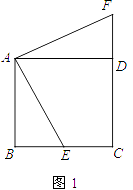
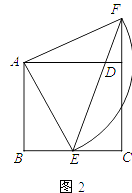
(2)解:①如图2,依题意,AE=AF,∠EAF=90°.
在Rt△ABE中,
∵AB=2,BE= ![]() BC=1,
BC=1,
∴AE= ![]() .
.
在Rt△AEF中,
EF= ![]() =
= ![]() =
= ![]() ;
;
②∵∠EAF=90°,AE=AF= ![]() ,
,
∴l= ![]() =
= ![]() π,
π,
∴弧EF的长为 ![]() π
π
【解析】(1)根据图形旋转的性质画出旋转后的图形即可;(2)①先根据勾股定理求出AE的长,由图形旋转的性质得出AF的长,根据勾股定理即可得出EF的长;②直接根据弧长公式即可得出结论.
【考点精析】通过灵活运用勾股定理的概念和弧长计算公式,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?