��Ŀ����
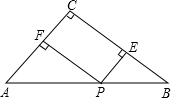 ��ͼ����֪��ABC�С�C=90�㣬BC=4��AC=3����P��б��AB�ϵ�һ���㣬��PE��BC�ڵ�E����PF��AC�ڵ�F������ֱ�ΪE��F��
��ͼ����֪��ABC�С�C=90�㣬BC=4��AC=3����P��б��AB�ϵ�һ���㣬��PE��BC�ڵ�E����PF��AC�ڵ�F������ֱ�ΪE��F����1����֤���ı���PECF�Ǿ��Σ�
��2����һ�룬����P�˶���ʲô�ط�ʱ����APF���PBEȫ�ȣ�֤����IJ��룻
��3����һ�룬����P�˶���ʲô�ط�ʱ���ı���PECF�������Σ�֤����IJ��룻
��4����һ�룬����P�˶���ʲô�ط�ʱ���ı���PECF�����������������ֵ��
��������1��֪��ʲô�Ǿ��μ�����⣬��ȷ���ĸ��Ƕ���ֱ�Ǽ��ɣ�
��2����ʹ��������ȫ�ȣ���Ϊ����ֱ�������Σ���PF��BC��ֻ��һ������ȼ��ɣ���P�˶����е�λ��ʱ������б����ȣ�
��3���ɣ�1��֪�ı���PECF�Ǿ��Σ�Ҫʹ��Ϊ�����Σ�ֻ�������������༴�ɣ��ȼ��������ڱ���ȣ���PE=PF���ڼ�����Ϊһδ֪��x��ͨ��������������������ֵ��
��4����һ���漰���κ�������ֵ���⣬���ȼ���AP=x���ɡ�APF�ס�ABC�����x��ֵ���������������������P���ƶ���AB�е�ʱ�����Ϊ���
��2����ʹ��������ȫ�ȣ���Ϊ����ֱ�������Σ���PF��BC��ֻ��һ������ȼ��ɣ���P�˶����е�λ��ʱ������б����ȣ�
��3���ɣ�1��֪�ı���PECF�Ǿ��Σ�Ҫʹ��Ϊ�����Σ�ֻ�������������༴�ɣ��ȼ��������ڱ���ȣ���PE=PF���ڼ�����Ϊһδ֪��x��ͨ��������������������ֵ��
��4����һ���漰���κ�������ֵ���⣬���ȼ���AP=x���ɡ�APF�ס�ABC�����x��ֵ���������������������P���ƶ���AB�е�ʱ�����Ϊ���
����⣺��1��֤������PE��BC��
���PEC=90�㣨1�֣�
ͬ������PFC=��C=90�㣬
���ı���PECF�Ǿ��Σ�����������ֱ�ǵ��ı����Ǿ��Σ�����2�֣�
��2��P�˶����߶�AB���е�ʱ����APF���PBEȫ�ȣ�3�֣�
��PE��BC��
���PEB=��C=90�㣬
��PE��AC��
���EPB=��A��4�֣�
ͬ����APF=��B��
����P��AB�������AP=PB��
�ɵá�APF�ա�PBE��ASA������5�֣�
��3����AP=
ʱ���ı���PECF�������Σ�
�ɣ�1��֪�ı���PECF�Ǿ��Σ����ı���PECF�������Σ�
����PE=PF����PE=PF=x��
��CF=x��AF=3-x����6�֣�
��PE��AC��
���BEP=��C����BPE=��A��
���APF�ס�ABC����7�֣�
��
=
=
����
=
��
���x=
��
������x=
�Ƿ��̵ĸ���
��AF=3-x=
��CF=x=
��
��Rt��AFP�У����ݹ��ɶ����ã�AP=
=
��
����AP=
ʱ��PE=PF=
��
����PECF��������
��4����AP=
ʱ���ı���PECF��������
�ɣ�1��֪�ı���PECF�Ǿ��Σ�
�ߡ�C=90�㣬BC=4��AC=3��
����ݹ��ɶ����ã�AB=
=5����9�֣�
��AP=x�����ɡ�APF�ס�ABC�ɵã�
=
=
����PF=
x��
=
=
����AF=
x��
��PE=3-
x��
��S����PECF=PF•FC=
x��3-
x����10�֣�
��
x��3-
x��=-
��x-
��2+3��
�൱x=
ʱ�ı���PECF�����������ֵΪ3����11�֣�
���PEC=90�㣨1�֣�
ͬ������PFC=��C=90�㣬
���ı���PECF�Ǿ��Σ�����������ֱ�ǵ��ı����Ǿ��Σ�����2�֣�
��2��P�˶����߶�AB���е�ʱ����APF���PBEȫ�ȣ�3�֣�
��PE��BC��
���PEB=��C=90�㣬
��PE��AC��
���EPB=��A��4�֣�
ͬ����APF=��B��
����P��AB�������AP=PB��
�ɵá�APF�ա�PBE��ASA������5�֣�
��3����AP=
| 15 |
| 7 |
�ɣ�1��֪�ı���PECF�Ǿ��Σ����ı���PECF�������Σ�
����PE=PF����PE=PF=x��
��CF=x��AF=3-x����6�֣�
��PE��AC��
���BEP=��C����BPE=��A��
���APF�ס�ABC����7�֣�
��
| PF |
| AF |
| BC |
| AC |
| 4 |
| 3 |
| x |
| 3-x |
| 4 |
| 3 |
���x=
| 12 |
| 7 |
������x=
| 12 |
| 7 |
��AF=3-x=
| 9 |
| 7 |
| 12 |
| 7 |
��Rt��AFP�У����ݹ��ɶ����ã�AP=
| AF2+PF2 |
| 15 |
| 7 |
����AP=
| 15 |
| 7 |
| 12 |
| 7 |
����PECF��������
��4����AP=
| 5 |
| 2 |
�ɣ�1��֪�ı���PECF�Ǿ��Σ�
�ߡ�C=90�㣬BC=4��AC=3��
����ݹ��ɶ����ã�AB=
| AC2+BC2 |
��AP=x�����ɡ�APF�ס�ABC�ɵã�
| PF |
| AP |
| BC |
| AB |
| 4 |
| 5 |
| 4 |
| 5 |
| AF |
| AP |
| AC |
| AB |
| 3 |
| 5 |
| 3 |
| 5 |
��PE=3-
| 3 |
| 5 |
��S����PECF=PF•FC=
| 4 |
| 5 |
| 3 |
| 5 |
��
| 4 |
| 5 |
| 3 |
| 5 |
| 12 |
| 25 |
| 5 |
| 2 |
�൱x=
| 5 |
| 2 |
�������������������μ����ε����ʼ��ж�������ֱ�������ι��ɶ����ĸ���ܹ������κ�������ֵ���⣮

��ϰ��ϵ�д�
 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
�����Ŀ
 ��ͼ����֪��ABC�У�AB=AC��E��F�ֱ���AB��AC����AE=CF��
��ͼ����֪��ABC�У�AB=AC��E��F�ֱ���AB��AC����AE=CF��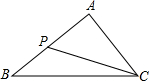 ��ͼ����֪��ABC�У�P��AB��һ�㣬����CP���������������ж���ACP�ס�ABC���ǣ�������
��ͼ����֪��ABC�У�P��AB��һ�㣬����CP���������������ж���ACP�ס�ABC���ǣ������� ��2012•������һģ����ͼ����֪��ABC�У���C=90�㣬AC=4��BC=3����sinA=��������
��2012•������һģ����ͼ����֪��ABC�У���C=90�㣬AC=4��BC=3����sinA=�������� ��ͼ����֪��ABC�У�BC=8��BC���ϵĸ�h=4��DΪBC��һ�㣬EF��BC��AB��E����AC��F��EF����A��B������E��BC�ľ���Ϊx����DEF�����Ϊy����ôy����x�ĺ���ͼ������ǣ�������
��ͼ����֪��ABC�У�BC=8��BC���ϵĸ�h=4��DΪBC��һ�㣬EF��BC��AB��E����AC��F��EF����A��B������E��BC�ľ���Ϊx����DEF�����Ϊy����ôy����x�ĺ���ͼ������ǣ������� ��ͼ����֪��ABC�У�AB=AC��D��BC�е㣬�����н��۲���ȷ���ǣ�������
��ͼ����֪��ABC�У�AB=AC��D��BC�е㣬�����н��۲���ȷ���ǣ�������