题目内容
 如图,正方形ABCD的边长为
如图,正方形ABCD的边长为 ,E是边AD上的一个动点(不与A重合),BE交对角线于F,连接DF.
,E是边AD上的一个动点(不与A重合),BE交对角线于F,连接DF.
(1)求证:BF=DF;
(2)设AF=x,△ABF面积为y,求y与x的函数关系式,并画出图象.
(1)证明:∵四边形ABCD为正方形,
∴∠BAC=∠DAC=45°,AB=AD,
在△ABF和△ADF中,
∵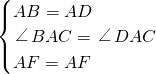 ,
,
∴△ABF≌△ADF(SAS),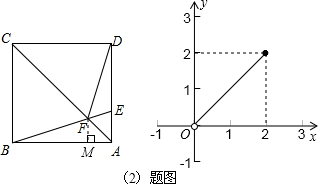
∴BF=DF;
(2)解:如图,过点F作FM⊥AB,
∵∠BAC=45°(正方形的对角线平分一组对角),
∴FM= AF=
AF= x,
x,
∴y= AB•FM=
AB•FM= ×2
×2 ×
× x=x,
x=x,
∵E是边AD上的一个动点,
∴AF的最大值为 AC=
AC= ×
× AB=
AB= ×
× ×2
×2 =2,
=2,
∴自变量的取值范围是0<x≤2,
故y与x的函数关系式为y=x(0<x≤2),图象如图.
分析:(1)根据正方形的对角线平分一组对角可得∠BAC=∠DAC=45°,根据正方形的四条边都相等可得AB=AD,然后利用“边角边”证明△ABF和△ADF全等,根据全等三角形对应边相等即可得证;
(2)过点F作FM⊥AB于点M,根据正方形的性质以及等腰直角三角形的性质求出FM的长度,再利用三角形的面积公式列式整理即可得到y与x的函数关系式.
点评:本题考查了正方形的性质,全等三角形的判定与性质,以及作正比例函数图象,比较简单,(2)中作辅助线构造等腰直角三角形从而求出AB边上的高是解题的关键,要注意自变量的取值范围.
∴∠BAC=∠DAC=45°,AB=AD,
在△ABF和△ADF中,
∵
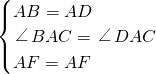 ,
,∴△ABF≌△ADF(SAS),

∴BF=DF;
(2)解:如图,过点F作FM⊥AB,
∵∠BAC=45°(正方形的对角线平分一组对角),
∴FM=
 AF=
AF= x,
x,∴y=
 AB•FM=
AB•FM= ×2
×2 ×
× x=x,
x=x,∵E是边AD上的一个动点,
∴AF的最大值为
 AC=
AC= ×
× AB=
AB= ×
× ×2
×2 =2,
=2,∴自变量的取值范围是0<x≤2,
故y与x的函数关系式为y=x(0<x≤2),图象如图.
分析:(1)根据正方形的对角线平分一组对角可得∠BAC=∠DAC=45°,根据正方形的四条边都相等可得AB=AD,然后利用“边角边”证明△ABF和△ADF全等,根据全等三角形对应边相等即可得证;
(2)过点F作FM⊥AB于点M,根据正方形的性质以及等腰直角三角形的性质求出FM的长度,再利用三角形的面积公式列式整理即可得到y与x的函数关系式.
点评:本题考查了正方形的性质,全等三角形的判定与性质,以及作正比例函数图象,比较简单,(2)中作辅助线构造等腰直角三角形从而求出AB边上的高是解题的关键,要注意自变量的取值范围.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2. 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE= 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.