题目内容
已知正比例函数y=kx的图象与反比例函数y=| 5-k |
| x |
(1)求两个函数图象的交点坐标;
(2)若点A(x1,y1),B(x2,y2)是反比例函数y=
| 5-k |
| x |
分析:(1)交点的坐标就是方程组
的解,把X=2代入解次方程组即得交点坐标;
(2)根据反比例函数的增减性和图象位置,通过分类讨论,就能比较y1,y2的大小.
|
(2)根据反比例函数的增减性和图象位置,通过分类讨论,就能比较y1,y2的大小.
解答:解:(1)将x=2代入正比例函数y=kx的图象与反比例函数y=
中,得:2k=
,
解得:k=1.
∴正比例函数的表达式为y=x,反比例函数的表达式为y=
.
∴x=
,
即x2=4,
得x=±2.
∴两函数图象交点的坐标为(2,2),(-2,-2);
(2)∵反比例函数y=
的图象分别在第一,三象限内,在每一象限内y的值随x值的增大而减小,
∴当x1<x2<0时,y1>y2.
当x1<0<x2时,因为y1=
<0,y2=
>0,所以y1<y2.
当0<x1<x2,时,y1>y2.
| 5-k |
| x |
| 5-k |
| 2 |
解得:k=1.
∴正比例函数的表达式为y=x,反比例函数的表达式为y=
| 4 |
| x |
∴x=
| 4 |
| x |
即x2=4,
得x=±2.
∴两函数图象交点的坐标为(2,2),(-2,-2);
(2)∵反比例函数y=
| 4 |
| x |
∴当x1<x2<0时,y1>y2.
当x1<0<x2时,因为y1=
| 4 |
| x1 |
| 4 |
| x2 |
当0<x1<x2,时,y1>y2.
点评:本题考查了反比例函数的综合应用,能够熟练根据解析式求得点的坐标是解决此题的关键.

练习册系列答案
相关题目
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
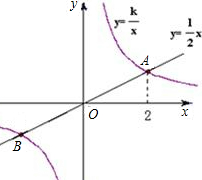 横坐标为2.
横坐标为2. 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).