��Ŀ����
����Ŀ�����ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ��������ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=����멁�����ѣ�
��2����ÿ�վ�����ΪwԪ����д��w��x֮��ĺ�����ϵʽ��
��3����ij�յľ�����Ϊ4420Ԫ����ʹ�ο͵õ�ʵ�ݣ�����Ĺ۹��������Ƕ���Ԫ��
���𰸡�
��1���⣺������֪��
���۹��ȫ���������0��x��100��
50x��1100��0��
���x��22��
�֡�x��5�ı�����
��ÿ���������������ӦΪ25Ԫ
��2���⣺��ÿ�����ľ�����ΪwԪ��
�൱0��x��100ʱ��w1=50x��1100��
��x��100ʱ��w2=x��50�� ![]() ����1100=��
����1100=�� ![]() x2+70x��1100��
x2+70x��1100��
��w= 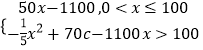
��3���⣺��w=4420��
�൱0��x��100ʱ��
50x��1100=4420��
��x=110.4����ȥ����
��x��100ʱ���У�
�� ![]() x2+70x��1100=4420��
x2+70x��1100=4420��
��ã�x1=230��x2=120��
��ʹ�ο͵õ�ʵ�ݣ�����Ĺ۹���������120Ԫ
����������1��������������г���Ӧ�IJ���ʽ���Ӷ��������ÿ���������������ӦΪ����Ԫ����2������������Եõ�w��x�ĺ�����ϵʽ����3��������ͣ�2���е������������ʹ�ο͵õ�ʵ�ݣ�����Ĺ۹�������

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�