题目内容
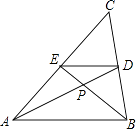
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E. 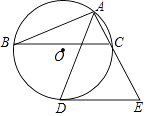
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
【答案】
(1)解:DE与⊙O相切,
理由:连接DO并延长到圆上一点N,交BC于点F,
∵AD平分∠BAC交⊙O于点D,
∴∠BAD=∠DAC,
∴ ![]() ,
,
∴DO⊥BC,
∵DE∥BC,
∴∠EDO=90°,
∴DE与⊙O相切
(2)解:连接AO并延长到圆上一点M,连接BM,

∵BC∥DE,
∴∠ACB=∠E=60°,
∴∠M=60°,
∵⊙O的半径为5,
∴AM=10,
∴BM=5,则AB= ![]() =5
=5 ![]() .
.
【解析】(1)利用垂径定理的推论结合平行线的性质得出∠EDO=90°,进而得出答案;(2)结合已知利用圆周角定理以及勾股定理得出AB的长.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
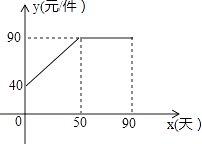
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.