题目内容
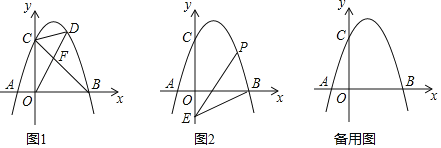
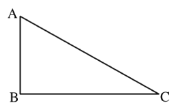
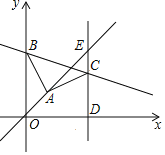
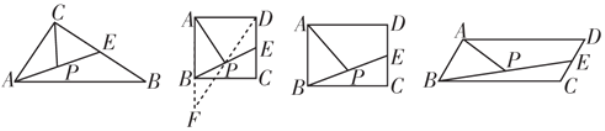
【题目】(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,则称CP是△ABC的“双中线”.若∠ACB=90°,AC=3,AB=5,则CP=________;
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”.若AB=4,则AP的长为__________;(按图示辅助线求解)
(3)在图3中,AP是矩形ABCD的“双中线”.若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
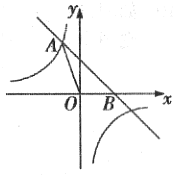
(4)在图4中,AP是□ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°,求△ABP的周长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)AP的长为
;(3)AP的长为![]() ,理由见解析;(4)4+
,理由见解析;(4)4+![]() +
+![]() .
.
【解析】
(1)利用勾股定理求出BC、AE,再利用直角三角形斜边上的中线等于斜边的一半即可求出结论;
(2)连接DP并延长交AB的延长线于F,利用AAS证出△FBP≌△DEP,从而求出AF和AD,利用勾股定理求出DF,再利用直角三角形斜边上的中线等于斜边的一半即可求出结论;
(3)连接DP并延长交AB的延长线于点H,利用AAS证出△PBH≌△PED,从而求出AH和AD,利用勾股定理求出DH,再利用直角三角形斜边上的中线等于斜边的一半即可求出结论;
(4)连接DP并延长交AB的延长线于点H,作DK⊥BA交BA的延长线于点K,过点A作AN⊥DH于点N,过点E作EM⊥BC交BC的延长线于点M,利用勾股定理、锐角三角函数和相似三角形的判定及性质求出PB和PA即可求出结论.
解:(1)∵∠ACB=90°,AC=3,AB=5,
∴BC=![]()
∵E是BC的中点,
∴CE=![]() BC=2
BC=2
∴AE=![]()
∵P是AE的中点,
∴CP=![]() AE=
AE=![]()
故答案为: ![]() ;
;
(2)连接DP并延长交AB的延长线于F
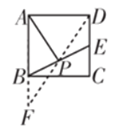
∵E是正方形ABCD一边上的中点,AB=4
∴AB=CD=AD=4,AB∥CD,∠BAD=90°
∴DE=![]() CD=2,∠F=∠PDE,∠FBP=∠DEP
CD=2,∠F=∠PDE,∠FBP=∠DEP
∵P是BE上的中点,
∴BP=EP
∴△FBP≌△DEP
∴FP=DP,BF=DE=2
∴AF=AB+BF=6
在Rt△ADF中,DF=![]()
∴AP=![]() DF=
DF=![]()
故答案为:![]() ;
;
(3)AP的长为![]() ,理由如下:
,理由如下:
如下图,连接DP并延长交AB的延长线于点H.
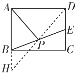
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD=4,AD=BC=6,∠HAD=90°.
∴∠H=∠PDE.
∵P是BE上的中点,
∴BP=EP.
又∠BPH=∠EPD,
∴△PBH≌△PED(AAS).
∴BH=ED,HP=DP.
∵E是CD的中点,
∴BH=ED=CD=2.
∴AH=AB+BH=6.
在Rt△ADH中,DH=![]() ,
,
∴AP=![]() DH=
DH=![]() .
.
(4)如下图,连接DP并延长交AB的延长线于点H,作DK⊥BA交BA的延长线于点K,过点A作AN⊥DH于点N,过点E作EM⊥BC交BC的延长线于点M.
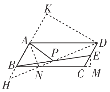
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,CD=AB=4,AD=BC=10.
在Rt△ADK中,∠KAD=180°-∠BAD=60°,∠K=90°,AD=10,
∴AK=AD·cos 60°=5,KD=AD·sin 60°=![]() .
.
在Rt△ECM中,∠M=90°,∠ECM=180°-∠BCD=60°,EC=![]() CD=2,
CD=2,
∴CM=EC·cos 60°=1,EM=EC·sin 60°=![]() .
.
在Rt△BEM中,BM=BC+CM=11,
∴BE=![]() =
=![]() .
.
∵P是BE的中点,
∴PB=![]() BE=
BE=![]() .
.
同(3)可得△PBH≌△PED,
∴HP=DP,HB=DE=![]() CD=2.
CD=2.
∴HK=HB+AB+AK=2+4+5=11,AH=AB+BH=6.
在Rt△HKD中,DH=![]() =14,
=14,
∴PH=PD=![]() DH=7.
DH=7.
∵∠AHN=∠DHK,∠ANH=∠K=90°,
∴△HAN∽△HDK.
∴![]() .
.
∴![]() .
.
∴AN=![]() ,HN=
,HN=![]() .
.
∴PN=PH-HN=7-![]() =
=![]() .
.
在Rt△APN中,PA=![]() =
= ,
,
∴△ABP的周长=AB+PA+PB=4+![]() +
+![]() .
.