题目内容
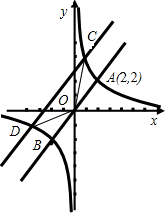 如图,在直角坐标系中,直线OA与双曲线交于点A(2,2),
如图,在直角坐标系中,直线OA与双曲线交于点A(2,2),求:(1)直线OA与双曲线的函数解析式;
(2)将直线OA向上平移3个单位后,求△COD的面积.
分析:(1)根据待定系数法就可以求出函数的解析式;
(2)在(1)的基础上,根据函数图象平移的法则“左加右减,上加下减”,就可以求出平移以后函数的解析式,进一步联立解方程组,求得交点的坐标;利用直线与y轴的交点运用分割法求得三角形的面积.
(2)在(1)的基础上,根据函数图象平移的法则“左加右减,上加下减”,就可以求出平移以后函数的解析式,进一步联立解方程组,求得交点的坐标;利用直线与y轴的交点运用分割法求得三角形的面积.
解答:解:(1)设直线的解析式是y=mx;设双曲线的解析式是y=
.
则2m=2,m=1;k=2×2=4.
∴直线OA的函数解析式y=x;
双曲线的函数解析式y=
.
(2)将直线OA向上平移3个单位后,则直线CD解析式为y=x+3.
根据题意,得
,
解得
或
.
得交点C(1,4),D(-4,-1).
设直线CD与y轴交点为E,则点E(0,3).
∴S△COD=S△COE+S△EOD=
+
=7.5.
| k |
| x |
则2m=2,m=1;k=2×2=4.
∴直线OA的函数解析式y=x;
双曲线的函数解析式y=
| 4 |
| x |
(2)将直线OA向上平移3个单位后,则直线CD解析式为y=x+3.
根据题意,得
|
解得
|
|
得交点C(1,4),D(-4,-1).
设直线CD与y轴交点为E,则点E(0,3).
∴S△COD=S△COE+S△EOD=
| 3×1 |
| 2 |
| 3×4 |
| 2 |
点评:本题要注意利用一次函数的特点,列出方程组,求出未知数的值从而求得其解析式;求直线平移后的解析式时要注意平移时k的值不变.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: