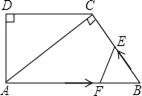
题目内容
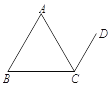
【题目】如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=![]() AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.

A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,④正确;
由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;
证出OG是△ABD的中位线,得出OG∥AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;③不正确;即可得出结果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;③不正确;即可得出结果.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
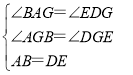 ,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
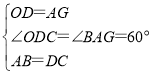 ,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴S四边形ODGF=S△ABF;③不正确;
正确的是①④.
故选B.

【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的![]() 型车2018年6月份销售总额为
型车2018年6月份销售总额为![]() 万元,今年经过改造升级后
万元,今年经过改造升级后![]() 型车每辆销售价比去年增加
型车每辆销售价比去年增加![]() 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
(1)今年6月份![]() 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)
(2)已知![]() 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表:
|
| |
进货价格(元/辆) |
|
|
销售价格(元/辆) | 今年的销售价格 |
|
该车行计划7月份进这批![]() 型车和
型车和![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多?