题目内容
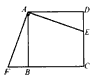
已知如图，在正方形ABCD的各边上向形内作120°弧，连结各交点得正方形A′B′C′D′．求SA′B′C′D′与SABCD的比值．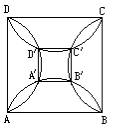
答案：
解析：
提示：
解析：
| 1∶3
|
提示：
| 连接AA′，BB′．因为正方形关于对角线对称，所以 A′，B′各在对角线上．因为∠A′AB=∠B′BA=45°，
|
练习册系列答案
相关题目
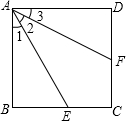已知如图，在正方形ABCD中，∠1=∠2=∠3，AE=4，则正方形的边长为（ ）| A、12 | ||
B、
| ||
| C、2 | ||
| D、无法计算 |
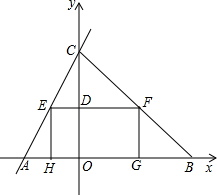已知如图，在平面直角坐标系中，A（-4，0），B（8，0），C（0，8），E为△ABC中AC边上一动点（不和A、C重合），以E为一顶点作矩形EFGH，使G、H点在x轴上，F点在BC上，EF交y轴于D点．并设EH长为x．
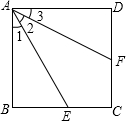已知如图，在正方形ABCD中，∠1=∠2=∠3，AE=4，则正方形的边长为
