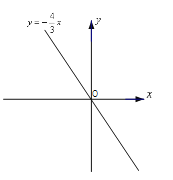
题目内容
【题目】如图①,已知AB是⊙O的直径,点D是线段AB延长线上的一个动点,直线DF垂直于射线AB于点D,当直线DF绕点D逆时针旋转时,与⊙O交于点C,且运动过程中,保持CD=OA
(1)当直线DF与⊙O相切于点C时,求旋转角的度数;
(2)当直线DF与半圆O相交于点C时(如图②),设另一交点为E,连接AE,OC,若AE∥OC.
①AE与OD的大小有什么关系?说明理由.
②求此时旋转角的度数.

【答案】(1)45°;(2)①结论:AE=OD.②∠CDF=54°
【解析】
(1)连接OC,因为CD是⊙O的切线,得出∠OCD=90°,由OC=CD,得出∠ODC=∠COD=45°即可解决问题;
(2)连接OE,①证明△AOE≌△OCD,即可得AE=OD;
②利用等腰三角形及平行线的性质,根据三角形内角和定理构建方程可求得∠ODC的度数,即可解决问题;
(1)如图①,连接OC.
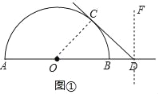
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
∴旋转角∠CDF=90°﹣45°=45°.
(2)如图②,连接OE.
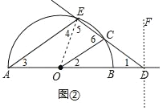
∵CD=OA,
∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°﹣2x.
①结论:AE=OD.理由如下:
在△AOE与△OCD中,
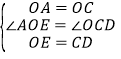 ,
,
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∵∠6=∠1+∠2=2x.OE=OC,
∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°,
∴旋转角∠CDF=54°.

【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.