题目内容
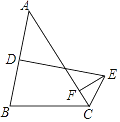
【题目】如图,△ABC中,D是AB的中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥AC交AC于F,AC=12,BC=8,则AF=________.
【答案】10
【解析】连接AE,BE,过E作EG⊥BC于G,

∵D是AB的中点,DE⊥AB,
∴DE垂直平分AB,
∴AE=BE,
∵∠ACE+∠BCE=180°,∠ECG+∠BCE=180°,
∴∠ACE=∠ECG,
又∵EF⊥AC,EG⊥BC,
∴EF=EG,∠FEC=∠GEC,
∵CF⊥EF,CG⊥EG,
∴CF=CG,
在Rt△AEF和Rt△BEG中,
![]() ,
,
∴Rt△AEF≌Rt△BEG(HL),
∴AF=BG,
设CF=CG=x,则AF=AC﹣CF=12﹣x,BG=BC+CG=8+x,
∴12﹣x=8+x,
解得x=2,
∴AF=12﹣2=10.

练习册系列答案
相关题目