题目内容
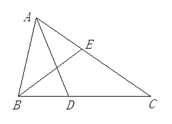
【题目】已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.
【答案】见解析
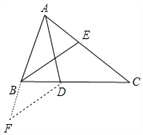
【解析】试题分析:延长AB到F,使BF=BD,连DF,即可得∠F=∠BDF;根据已知条件∠A:∠B:∠C=3:4:2和三角形的内角和定理即可求得∠ABC=80°,∠ACB=40°,再由三角形外角的性质求得∠F=40°,根据AAS证得△ADF≌△ADC,即可得AF=AC,再证得BE=EC,即可证得结论.
试题解析:
证明:延长AB到F,使BF=BD,连DF,
∴∠F=∠BDF,
∵∠A:∠B:∠C=3:4:2,
∴∠ABC=80°,∠ACB=40°,
∴∠F=40°,∠F=∠ACB,
∵AD是平分线,
∴∠BAD=∠CAD,
在△ADF和△ADC中,
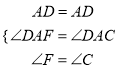 ,
,
∴△ADF≌△ADC,
∴AF=AC,
∵BE是角平分线,
∴∠CBE=![]() ∠ABC=40°
∠ABC=40°
∴∠EBD=∠C,
∴BE=EC,
∴BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.
∴AB+BD=AE+BE.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目