题目内容
【题目】矩形纸片ABCD中,AB=10,AD=8,将纸片折叠,使点B落在CD上的B′处,折痕为AE,在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等的距离为_____.
【答案】5
【解析】
根据题意画出图形,由折叠的性质得出F、B′重合,分别延长AE,DC交于点G,由平行线的性质可得出GB′=AB′=AB=10,再根据相似三角形的判定定理得出△ADG∽△PB′G,求出其相似比,进而可求出答案.
解:如图所示,设PF⊥CD,
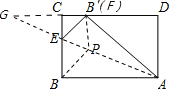
∵BP=FP,
由折叠的性质可得BP=B′P,
∴FP=B′P,
∵FP⊥CD,
∴B′,F,P三点构不成三角形,
∴F、B′重合,分别延长AE、DC交于点G,
∵AB平行于CD,
∴∠BAG=∠AGC,
∵∠BAG=∠B′AG,
∴∠AGC=∠B′AG,
∴GB′=AB′=AB=10,
∵PB′(PF)⊥CD,
∴PB′∥AD,
∴△ADG∽△PB′G,
∵Rt△ADB′中,AB′=10,AD=8,
∴DB′=6,DG=DB′+B′G=6+10=16,
∴△ADG与△PB′G的相似比为8:5,
∴AD:PB′=8:5,
∵AD=8,
∴PB′=5,即相等距离为5.
故答案为:5.

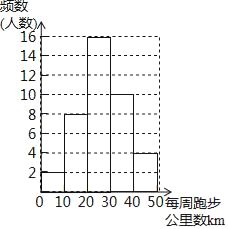
【题目】某市举行主题为“奔跑吧!2018”的市民健康跑活动.红树林学校的小记者随机采访了40名参赛选手,了解到他们平时每周跑步公里数(单位:km),并根据统计结果绘制出以下频数分布直方图和不完整的表格.
每周跑步公里数/km | 频数(人数) | 频率 |
0≤x<10 | 2 | 5% |
10≤x<20 | a | m |
20≤x<30 | b | 40% |
30≤x<40 | 10 | 25% |
40≤x<50 | 4 | n |
(1)求a= ,n= ;
(2)本次活动有10000人参加比赛,请根据上述调查结果,估算该活动中每周跑步公里数在10≤x<30 内的人数;
(3)应比赛组委会要求,现从每周跑步公里数在40≤x<50 内的4名参赛选手甲,乙,丙,丁中随机抽取2人作为本次活动的形象宣传员,请用画树状图法或列表法求出恰好抽中乙,丙两人的概率.