题目内容
【题目】如图,已知∠ABC=90°, D是直线AB上的点,AD=BC ,过点A作AF⊥AB,并截取AF=DB ,连接DC、DF、CF ,判断△CDF的形状并证明.

【答案】△![]() 是等腰直角三角形,证明见解析
是等腰直角三角形,证明见解析
【解析】
试题由“ASA”证明△ADF≌△BCD得到DF=CD,∠ADF=∠BCD,再利用∠BCD+∠CDB=90°得到∠CDF=90°,则可判断△CDF为等腰直角三角形.
试题解析:△![]() 是等腰直角三角形,
是等腰直角三角形,
证明如下:
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
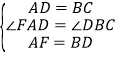 ,
,
∴△FAD≌△DBC(SAS);
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目






