题目内容
已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=| k |
| x |
| 3 |
| 5 |
(1)求k的值和边AC的长;
(2)求点B的坐标.
分析:(1)本题需先根据C点的坐标在反比例函数y=
的图象上,从而得出k的值,再根据且sin∠BAC=
,得出AC的长.
(2)本题需先根据已知条件,得出∠DAC=∠DCB,从而得出CD的长,根据点B的位置即可求出正确答案.
| k |
| x |
| 3 |
| 5 |
(2)本题需先根据已知条件,得出∠DAC=∠DCB,从而得出CD的长,根据点B的位置即可求出正确答案.
解答: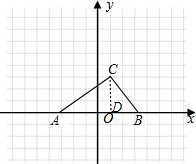 解:(1)∵点C(1,3)在反比例函数y=
解:(1)∵点C(1,3)在反比例函数y=
的图象上,
∴3=
,解得k=3,
∵sin∠BAC=
∴sin∠BAC=
=
∴AC=5;
∴k的值和边AC的长分别是:3,5.
(2)①当点B在点A右边时,如图,
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠DAC=∠DCB,
又∵sin∠BAC=
,
∴tan∠DAC=
,
∴
=
,
又∵CD=3,
∴BD=
,
∴OB=1+
=
,
∴B(
,0);
②当点B在点A左边时,如图,
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠DAC=∠DCB,
又∵sin∠BAC=
,
∴tan∠DAC=
,
∴
=
,
又∵CD=3,
∴BD=
,BO=BD-1=
,
∴B(-
,0)
∴点B的坐标是(-
,0),(
,0).
 解:(1)∵点C(1,3)在反比例函数y=
解:(1)∵点C(1,3)在反比例函数y=| k |
| x |
∴3=
| k |
| 1 |
∵sin∠BAC=
| 3 |
| 5 |
∴sin∠BAC=
| 3 |
| AC |
| 3 |
| 5 |
∴AC=5;
∴k的值和边AC的长分别是:3,5.
(2)①当点B在点A右边时,如图,
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠DAC=∠DCB,
又∵sin∠BAC=
| 3 |
| 5 |
∴tan∠DAC=
| 3 |
| 4 |
∴
| BD |
| CD |
| 3 |
| 4 |
又∵CD=3,
∴BD=
| 9 |
| 4 |
∴OB=1+
| 9 |
| 4 |
| 13 |
| 4 |
∴B(
| 13 |
| 4 |
②当点B在点A左边时,如图,
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠DAC=∠DCB,

又∵sin∠BAC=
| 3 |
| 5 |
∴tan∠DAC=
| 3 |
| 4 |
∴
| BD |
| CD |
| 3 |
| 4 |
又∵CD=3,
∴BD=
| 9 |
| 4 |
| 5 |
| 4 |
∴B(-
| 5 |
| 4 |
∴点B的坐标是(-
| 5 |
| 4 |
| 13 |
| 4 |
点评:本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系是本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
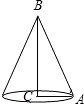 已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )
已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )| A、8π | B、12π | C、15π | D、20π |
已知Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm,以直线AB为轴旋转一周,得到的几何体的表面积是( )
| A、22.56πcm2 | B、16.8πcm2 | C、9.6πcm2 | D、7.2πcm2 |
