题目内容
已知Rt△ABC的斜边AB=5cm,直角边AC=3cm,则此三角形内切圆半径是分析:设三角形内切圆半径为r,由勾股定理得出BC=4,再根据三角形的面积等于周长乘以半径的一半,从而得出三角形内切圆半径.
解答:解:解法一:
设三角形内切圆半径为r,则
•r•(5+4+3)=
•3•4?r=1
解法二: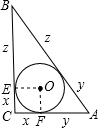
如图,引入参数x,y,z表示相应线段的长度,
则
?
易证OECF是正方形.
∴r=1.
故答案为:1.
设三角形内切圆半径为r,则
| 1 |
| 2 |
| 1 |
| 2 |
解法二:

如图,引入参数x,y,z表示相应线段的长度,
则
|
|
∴r=1.
故答案为:1.
点评:本题考查了三角形的内切圆和内心的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
 已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )
已知Rt△ABC的斜边AB=5,一条直角边AC=3,以直线BC为轴旋转一周得到一个圆锥,则这个圆锥的侧面积为( )| A、8π | B、12π | C、15π | D、20π |
已知Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm,以直线AB为轴旋转一周,得到的几何体的表面积是( )
| A、22.56πcm2 | B、16.8πcm2 | C、9.6πcm2 | D、7.2πcm2 |
