题目内容
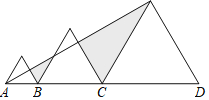
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是______.(把所有正确结论的序号都填在横线上)
(1)∠DFC+∠FEC=90°;(2)∠B=∠AEF;(3)CF=EF;(4)![]()
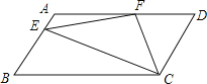
【答案】(1)(3)
【解析】
分别利用平行四边形的性质以及全等三角形的判定得出△AEF≌△DMF,得出角、线段之间关系,得出(1)(3)成立,(2)不成立;再由梯形面积和平行四边形面积关系进而得出(4)不成立.
解:∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
延长EF,交CD延长线于M,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
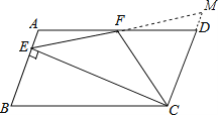
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,

∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵∠B=∠ADC>∠M,
∴∠B>∠AEF,(2)不成立;
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴CF=EF,(3)成立;
∴∠FEC=∠FCE,
∵∠DCF+∠FEC=90°,
∴∠DFC+∠FEC=90°,(1)成立;
∵四边形ADCE的面积=![]() (AE+CD)×CE,F是AD的中点,
(AE+CD)×CE,F是AD的中点,
∴S△EFC=![]() S四边形ADCE,
S四边形ADCE,
∵S△BDC=![]() S平行四边形ABCD=
S平行四边形ABCD=![]() CD×CE,
CD×CE,
∴S△EFC≠![]() S△BDC,(4)不成立;
S△BDC,(4)不成立;
故答案为:(1)(3).

 名校课堂系列答案
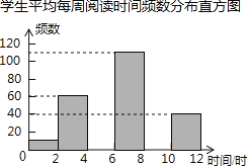
名校课堂系列答案【题目】为引导学生广泛阅读古今文学名著,某校开展了读书活动.学生会随机调查了部分学生平均每周阅读时间的情况,整理并绘制了如下的统计图表:
学生平均每周阅读时间频数分布表
平均每周阅读时间x(时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | b |
8≤x<10 | 100 | 0.250 |
10≤x≤12 | 40 | 0.100 |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题;
(1)在频数分布表中,a=______,b=______;
(2)补全频数分布直方图;
(3)如果该校有1600名学生,请你估计该校平均每周阅读时间不少于6小时的学生大约有多少人?