题目内容
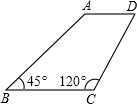 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
分析:作AE⊥BC于E点,DF⊥BC于F点,则有AE=DF,sinB=sin45°=
=
,由此可以求出DF、AE;
又sin∠DCF=sin60°=
,由此求出CD.
| AE |
| AB |
| ||
| 2 |
又sin∠DCF=sin60°=
| DF |
| CD |
解答: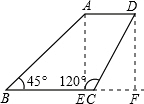 解:如图,分别作AE⊥BC于E点,DF⊥BC于F点.
解:如图,分别作AE⊥BC于E点,DF⊥BC于F点.
则有AE=DF,sinB=sin45°=
=
,
∴DF=AE=
AB=4
.
又∵sin∠DCF=sin60°=
=
,
∴CD=
=
=
.
故选A.
 解:如图,分别作AE⊥BC于E点,DF⊥BC于F点.
解:如图,分别作AE⊥BC于E点,DF⊥BC于F点.则有AE=DF,sinB=sin45°=
| AE |
| AB |
| ||
| 2 |
∴DF=AE=
| ||
| 2 |
| 2 |
又∵sin∠DCF=sin60°=
| DF |
| CD |
| ||
| 2 |
∴CD=
| DF | ||||
|
4
| ||||
|
8
| ||
| 3 |
故选A.
点评:此题主要考查通过作辅助线综合利用解直角三角形、直角三角形性质等知识解决问题,同时也考查学生逻辑推理能力和运算能力.

练习册系列答案
相关题目
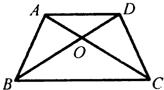 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )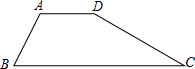 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=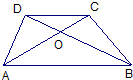 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=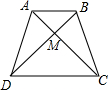 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.