题目内容
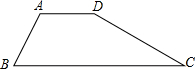 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
| ||
| 6 |
分析:过A、D作AE⊥BC于E、DF⊥BC于F,将梯形分为两个直角三角形和一个矩形,由∠DAB=120°得∠BAE=30°,设BE=
AB=x,则AE=
x,由tanC=
,得CF=6x,AD=EF=AB=2x,根据BC=18列方程求x,再求AD.
| 1 |
| 2 |
| 3 |
| ||
| 6 |
解答: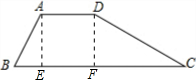 解:如图,过A、D作AE⊥BC于E、DF⊥BC于F
解:如图,过A、D作AE⊥BC于E、DF⊥BC于F
设AD=AB=2x
Rt△ABE中,∠BAE=120°-90°=30°
∴BE=
AB=x,AE=
x
Rt△DFC中,DF=AE=
x
∵tanC=
∴CF=
DF=6x
∵BC=18
∴x+2x+6x=18
解得x=2
∴AD=2x=4.
 解:如图,过A、D作AE⊥BC于E、DF⊥BC于F
解:如图,过A、D作AE⊥BC于E、DF⊥BC于F设AD=AB=2x
Rt△ABE中,∠BAE=120°-90°=30°
∴BE=
| 1 |
| 2 |
| 3 |
Rt△DFC中,DF=AE=
| 3 |
∵tanC=
| ||
| 6 |
∴CF=
| 6 | ||
|
∵BC=18
∴x+2x+6x=18
解得x=2
∴AD=2x=4.
点评:本题考查了梯形常用的作辅助线的方法,根据梯形高的“过渡”解直角三角形,列方程求解.

练习册系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )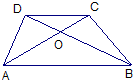 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.