题目内容
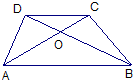8、已知，如图，梯形ABCD中，AB∥CD，△COD与△AOB的周长比为1：2，则CD：AB=1：2
，△COD与△BOC的面积比为1：4
．分析：由AB∥CD，判断△COD∽△AOB，根据相似三角形的周长比等于相似比，面积比等于相似比的平方求解．
解答：解：∵AB∥CD，∴△COD∽△AOB，
又，△COD与△AOB的周长比为1：2，
∴CD：AB=1：2，
△COD与△BOC的面积比为1：4．
故答案为：1：2，1：4．
又，△COD与△AOB的周长比为1：2，
∴CD：AB=1：2，
△COD与△BOC的面积比为1：4．
故答案为：1：2，1：4．
点评：本题考查了相似三角形的判定与性质．利用平行线可判断三角形相似，相似三角形的性质有：相似三角形对应边上高的比、对应边上中线的比、对应角的角平分线的比、周长比都等于相似比，面积比等于相似比的平方．
练习册系列答案
阅读快车系列答案
相关题目
9、已知：如图，梯形ABCD中，AD∥BC，AB=CD，对角线AC与BD相交于点O，则图中全等三角形共有（ ）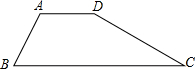
已知：如图，梯形ABCD中，AD∥BC，∠DAB=120°，tanC=
已知：如图，梯形ABCD中，AB∥CD，AD=BC，对角线AC、BD交于M，AB=2，CD=4，∠CMD=90°，求：BD的长．