Question

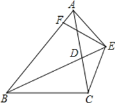
【题目】如图，在△ABC中，点D为BC边的任意一点，以点D为顶点的∠EDF的两边分别与边AB，AC交于点E、F，且∠EDF与∠A互补．

（1）如图1，若AB=AC，D为BC的中点时，则线段DE与DF有何数量关系？请直接写出结论；

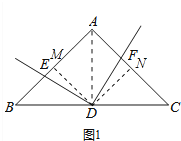
（2）如图2，若AB=kAC，D为BC的中点时，那么（1）中的结论是否还成立？若成立，请给出证明；若不成立，请写出DE与DF的关系并说明理由；

（3）如图3，若=a，且=b，直接写出=　 　．

Answer 1

【答案】(1) DF=DE; (2) DE：DF=1：k ; (3)

【解析】试题分析：（1）如图1，连接AD，作DM⊥AB于M，DN⊥AC于N，则∠EMD=∠FND=90°，只要证明△DEM≌△DFN即可．

（2）结论DE：DF=1：k．如图2，过点D作DM⊥AB于M，作DN⊥AC于N，连接AD，则∠EMD=∠FND=90°，由ABDM=ACDN，AB=kAC，推出DN=kDM，再证明

△DME∽△DNF，即可．

（3）结论DE：DF=1：k．如图3，过点D作DM⊥AB于M，作DN⊥AC于N，连接AD，同（2）可证∠EDM=∠FDN，由ABDM： ACDN=b，AB：AC=a，推出DM：DN=，再证明△DEM∽△DFN即可．

试题解析：（1）结论：DF=DE，

理由：如图1，连接AD，作DM⊥AB于M，DN⊥AC于N，则∠EMD=∠FND=90°，

∵AB=AC，点D为BC中点，

∴AD平分∠BAC，

∴DM=DN，

∵在四边形AMDN中．，∠DMA=∠DNA=90°，

∴∠MAN+∠MDN=180°，

又∵∠EDF与∠MAN互补，

∴∠MDN=∠EDF，

∴∠EDM=∠FDN，

在△DEM与△DFN中，

，

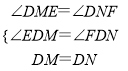∴△DEM≌△DFN，

∴DE=DF．

（2）结论DE：DF=1：k．

理由：如图2，过点D作DM⊥AB于M，作DN⊥AC于N，连接AD，则∠EMD=∠FND=90°，

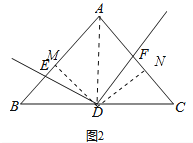
∵BD=DC，

∴S△ABD=S△ADC，

∴ABDM=ACDN，

∵AB=kAC，

∴DN=kDM，

由（2）可知，∠EDM=∠FDN，∠DEM=∠DFN=90°，

∴△DME∽△DNF，

∴

（3）结论： ．

理由：如图3，过点D作DM⊥AB于M，作DN⊥AC于N，连接AD，同（2）可证∠EDM=∠FDN，

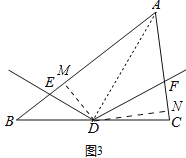
又∵∠EMD=∠FND=90°，

∴△DEM∽△DFN，

∴，

∵=b，

∴S△ABD：S△ADC=b，

∴ABDM： ACDN=b，

∵AB：AC=a，

∴DM：DN=，

∴．