题目内容
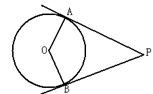
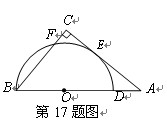
如图,⊙O的半径为5cm, AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
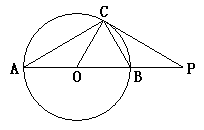
(1)求证:PC是⊙O的切线;(4分)
(2)求线段BC的长度.(4分)

(1)求证:PC是⊙O的切线;(4分)
(2)求线段BC的长度.(4分)
(1)证明略
(2)5cm
(1)证明:在⊙O中,∠COB=2∠CAB,OA=OC
∵OA=OC,∴∠CAB=∠ACO,∴∠COB=2∠ACO ————1分
又∵∠COB=2∠PCB,∴∠PCB=∠ACO
∵AB是⊙O的直径,∴∠ACB=90°,
即∠ACO+∠OCB=90°
∴∠PCB+∠OCB=90°,即∠OCP=90° ————2分
∴OC⊥CP
∴PC是⊙O的切线 ————1分
(2)解:∵⊙O的半径为5cm, AB是⊙O的直径,∴AB=10cm, ——1分
∵AC=PC,∴∠A=∠P,
∵∠COB=2∠A,∴∠COB=2∠P
又∵∠OCP=90°,∴∠COB+∠P=90°,
∴∠P=30°,
∴∠A=30°, —————2分
又∵∠ACB=90°,
∴CB=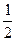 AB=5cm. —————1分
AB=5cm. —————1分
∵OA=OC,∴∠CAB=∠ACO,∴∠COB=2∠ACO ————1分
又∵∠COB=2∠PCB,∴∠PCB=∠ACO
∵AB是⊙O的直径,∴∠ACB=90°,
即∠ACO+∠OCB=90°
∴∠PCB+∠OCB=90°,即∠OCP=90° ————2分
∴OC⊥CP
∴PC是⊙O的切线 ————1分
(2)解:∵⊙O的半径为5cm, AB是⊙O的直径,∴AB=10cm, ——1分
∵AC=PC,∴∠A=∠P,
∵∠COB=2∠A,∴∠COB=2∠P
又∵∠OCP=90°,∴∠COB+∠P=90°,
∴∠P=30°,
∴∠A=30°, —————2分
又∵∠ACB=90°,
∴CB=
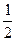 AB=5cm. —————1分
AB=5cm. —————1分
练习册系列答案
相关题目

 D.10
D.10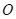 中,CD是直径,AB是弦,
中,CD是直径,AB是弦,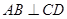 于M,
于M,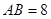 ,
,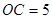 ,则MD的长为( )
,则MD的长为( )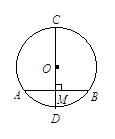
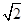
 m
m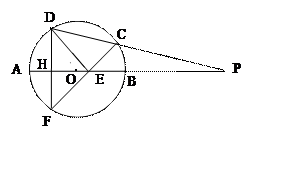
 的外接圆, 点
的外接圆, 点 在劣弧
在劣弧 上,
上, =22°,则
=22°,则 的度数为_________
的度数为_________