题目内容
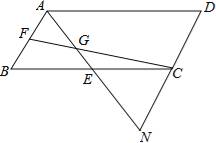
【题目】如图,在ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
(1)求证:△ABE≌△NCE;
(2)若AB=3n,FB=![]() GE,试用含n的式子表示线段AN的长.
GE,试用含n的式子表示线段AN的长.
【答案】(1)证明见解析
(2)6n
【解析】
试题(1)根据平行四边形的性质可得AB∥CN,由此可知∠B=∠ECN,再根据全等三角形的判定方法ASA即可证明△ABE≌△NCE;
(2)因为AB∥CN,所以△AFG∽△CNG,利用相似三角形的性质和已知条件即可得到含n的式子表示线段AN的长.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB∥CN,
∴∠B=∠ECN,
∵E是BC中点,
∴BE=CE,
又∵∠AEB=∠CEN,
∴△ABE≌△NCE
(2)∵△ABE≌△NCE,
∴AB=CN,AE=NE
∵AB∥CN,
∴△AFG∽△CNG,AF=![]()
∴AF:CN=AG:GN=1:2,
∵AE+NE=AG+GN,
∴AG=2GE,EN=3GE
∵AB=3n,FB=![]() GE=
GE=![]() ,
,
∴GE=n,AG=2n,EN=3n
∴AN=AG+GE+EN=6n.

【题目】某校八(1)班同学为了解2018年姜堰某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 12 | 0.24 |
10<x≤15 | m | 0.32 |
15<x≤20 | 10 | n |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
(1)本次调查采用的调杳方式是 (填“普査”或“抽样调查”),样本容量是 ;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“15<x≤20”的圆心角度数是 ;
(4)若该小区有5000户家庭,求该小区月均用水量超过20t的家庭大约有多少户?

【题目】某校组织九年级的三个班级进行趣味数学竞赛活动,各班根据初赛成绩分别选拔了10名同学参加决赛,决赛成绩(满分:10分)如下表所示:
班级 | 决赛成绩(单位:分) |
一班 | 5 5 6 7 7 8 8 8 9 10 |
二班 | 4 6 7 7 7 9 9 9 10 10 |
三班 | 5 6 7 7 8 9 9 9 10 10 |
根据以上信息完成下面的问题:
(1)把下表补充完整(单位:分),其中a= ,b= ,c= ;
班级 | 平均分 | 中位数 | 众数 |
一班 | 7.3 | a | 8 |
二班 | 7.8 | 8 | b |
三班 | c | 8.5 | 9 |
(2)各班在进行宣传时,都说自己班级决赛的成绩是8分,你如何理解他们的宣传?请用学过的统计量进行说明;
(3)为了在全市竞赛中取得好成绩,你认为应选派哪个班级代表学校去参加全市的竞赛?为什么?