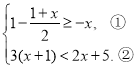Question

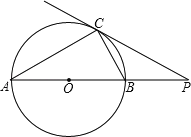
【题目】如图，点P在⊙O外，PC是⊙O的切线，C为切点，直线PO与⊙O相交于点A、B.

（1）若∠A＝30°，求证：PA＝3PB；

（2）小明发现，∠A在一定范围内变化时，始终有∠BCP＝（90°﹣∠P）成立.请你写出推理过程.

Answer 1

【答案】（1）见解析；（2）推理过程见解析.

【解析】

(1)由直径所对的圆周角是直角，以及∠A=30°可得∠ABC=60°，从而可判断△OBC是等边三角形，得到∠COB=60°，再结合切线的性质可求得∠P＝30°，继而可推得PB=OB，再根据AB=2OB，即可确定AP与BP的数量关系；

(2)连接OC，由圆周角定理以及切线的性质结合等角对等边可以推导得出∠BCP＝∠A，再由三角形内角和定理即可确定出两角的关系.

(1)连接OC，

∵AB是直径，

∴∠ACB＝90°，

又∵∠A=30°，

∴∠ABC=90°-30°=60°，

∵OB=OC，

∴△OBC是等边三角形，

∴OB=BC=OC，∠COB=60°，

∵PC是⊙O的切线，OC是半径，

∴∠OCP=90°，

∴∠P＝90°-∠BOC＝30°，

∴PO=2OC，

∴PB=OB，

∵AB=2OB，

∴AP=AB+PB=3PB；

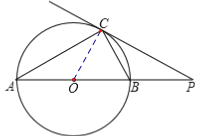
(2)如图，连接OC，

∵AB是直径，

∴∠ACB＝90°，即∠ACO+∠BCO=90°，

∵PC是⊙O的切线，OC是半径，

∴∠OCP=90°，即∠BCP+∠BCO=90°，

∴∠BCP=∠ACO，

∵OA=OC，

∴∠A=∠ACO，

∴∠BCP＝∠A，

∵∠A+∠P+∠ACB+∠BCP＝180°，且∠ACB＝90°，

∴2∠BCP＝180°﹣∠P，

∴∠BCP＝(90°﹣∠P).