题目内容
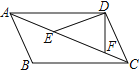
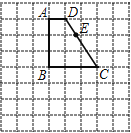
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形![]() 的顶点在格点上,点
的顶点在格点上,点![]() 是边
是边![]() 与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由
与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由
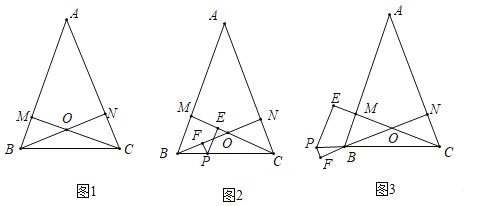
(1)如图1,过点![]() 画线段
画线段![]() ,使
,使![]() ,且
,且![]()
(2)如图1,在边![]() 上画一点
上画一点![]() ,使
,使![]()
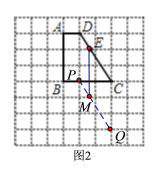
(3)如图2,过点![]() 画线段
画线段![]() ,使
,使![]() ,且
,且![]()

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)观察可知点D向左平移一个格得到点A,根据平移的性质,只要找到点C向左平移一个格后对应的点F,连接AF即可(根据一组对边平行且相等的四边形是平行四边形可得四边形ADCF是平行四边形,继而根据平行四边形的性质即可求得AF//DC,AF=DC);
(2)结合网格特点找到点C关于直线AB的对称点N,连接DN,DN与AB的交点即为点G(根据轴对称的性质可得∠BGC=∠BGN,又∠BGN=∠AGD,根据等量代换即可得∠AGD=∠BGC);
(3)根据网格的特点,观察可知点D向下平移3格后的对应点P在BC上,由此将点C向下平移3格得到对应点Q,连接PQ,PQ与网格线的交点中靠近BC的为点M,连接EM即可(根据画法可知四边形ABPD是矩形,四边形PDEM是平行四边形,由此即可得DM//AB,DM=AB).
(1)画图如图1所示;
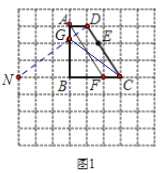
(2)画图如图1所示;
(3)画图如图2所示.

 开心蛙状元测试卷系列答案
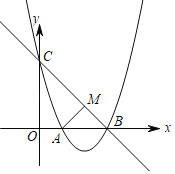
开心蛙状元测试卷系列答案【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.