��Ŀ����
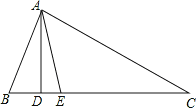
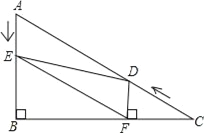
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬BC=5![]() ����C=30������D�ӵ�C������CA������ÿ��2����λ�����ٶ���A�������˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ�����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��
����C=30������D�ӵ�C������CA������ÿ��2����λ�����ٶ���A�������˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ�����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루t��0��������D��DF��BC�ڵ�F������DE��EF��
��1��AC�ij������� ��AB�ij����� ��
��2����D��E���˶������У��߶�EF��AD�Ĺ�ϵ�Ƿ����仯�������仯����ô�߶�EF��AD�Ǻι�ϵ��������֤�������仯����˵�����ɣ�
��3����tΪ��ֵ����BEF�������2![]() ��
��
���𰸡���1��10��5����2��EF��ADƽ������ȣ���3��3.
��������������(1)�����ݺ���30��ǵ�ֱ�������ε������Լ�BC�ij������AC��AB�ij��ȣ�(2)�������˶����ٶȵó�AE=DF�����ݴ�ֱ�ó�AE��DF���Ӷ��ó��ı���AEFDΪƽ���ı��Σ��Ӷ��ó�EF��AD�Ĺ�ϵ��(3)�������˶����ٶ��ú�t�Ĵ���ʽ��ʾBE��BF�ij��ȣ�Ȼ�����ֱ�������ε�������㷨��ó�t��ֵ��
��⣺��1���⣺����Rt��ABC�У���C=30�㣬 ��AC=2AB��
���ݹ��ɶ����ã�AC2��AB2=BC2�� ��3AB2=75�� ��AB=5��AC=10��
��2��EF��ADƽ������ȣ�
֤��������DFC�У���DFC=90�㣬��C=30�㣬DC=2t�� ��DF=t�� �֡�AE=t��
��AE=DF�� ��AB��BC��DF��BC�� ��AE��DF��
���ı���AEFDΪƽ���ı��Σ� ��EF��ADƽ������ȣ�
��3���⣺����Rt��CDF�У���A=30�㣬 ��DF=![]() CD�� ��CF=
CD�� ��CF=![]() t��
t��
�֡�BE=AB��AE=5��t��BF=BC��CF=5![]() ��
��![]() t��
t��
��![]() �� ����
�� ����![]() ��
��
��ã�t=3��t=7������������ȥ���� ��t=3��
�ʵ�t=3ʱ����BEF�����Ϊ2![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�