题目内容
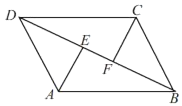
【题目】如图,已知BD是ABCD对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)求证:△ADE≌△CBF;
(2)连结CE,AF,求证:四边形AFCE为平行四边形.
【答案】(1)证明见解析;(2)结论:四边形AECF是平行四边形.理由见解析.
【解析】
(1)利用平行四边形的性质,根据ASA即可证明;
(2)首先证明四边形AECF是平行四边形.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥AD,
∴∠EAD=90°,同理∠BCF=90°.
∴∠EAD=∠BCF.
在△AED和△CFB中
∠ADB=∠CBD,AD=BC,∠EAD=∠BCF,
∴△ADE≌△CBF.
(2)结论:四边形AECF是平行四边形.
理由:连接AC,
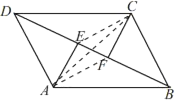
∵四边形ABCD是平行四边形,
∴AC平分BD,
由(1)△ADE≌△CBF,
∴AE=CF,∠AED=∠BFC,
∴AE∥CF,
∴四边形AECF是平行四边形.

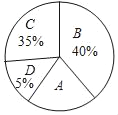
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.
【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?