Question

【题目】若数a使关于x的不等式组 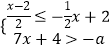有且仅有四个整数解，且使关于y的分式方程 + =2有非负数解，则所以满足条件的整数a的值之和是（ ）
A.3
B.1
C.0
D.﹣3

Answer 1

【答案】A
【解析】解：解不等式组 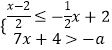，可得 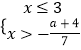， ∵不等式组有且仅有四个整数解，
∴﹣ ≥﹣1，
∴a≤3，
解分式方程 + =2，可得y= （a+2），
又∵分式方程有非负数解，
∴y≥0，
即 （a+2）≥0，
解得a≥﹣2，
∴﹣2≤a≤3，
∴满足条件的整数a的值为﹣2，﹣1，0，1，2，3，
∴满足条件的整数a的值之和是3，
故选：A．
【考点精析】通过灵活运用分式方程的解和一元一次不等式组的整数解，掌握分式方程无解（转化成整式方程来解,产生了增根;转化的整式方程无解）；解的正负情况:先化为整式方程,求整式方程的解；使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)即可以解答此题．