题目内容
(2009•扬州模拟)设关于x的一元二次方程x2+2 x+b=0(a≥0).
x+b=0(a≥0).(1)a,b为什么关系时,方程有实数根;
(2)若a是从1、2、3三个数中任取一个数,b是从2、3两个数中任取一个数,求上述方程有实数根的概率.
【答案】分析:(1)若一元二次方程有实数根,则根的判别式△≥0,解出a,b之间的关系;
(2)根据(1)中所得出的a,b之间的关系,从a,b值中选取合适的值,再分析方程有实数根的概率.
解答:解:(1)∵方程有实数根
∴△≥0
∴(2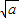 )2-4b≥0
)2-4b≥0
∴4a-4b≥0
∴a-b≥0
∴当a-b≥0时,方程有实数根.
(2)由(1)可知:有以下几种可能方程有实数根
a取2,b取2时,
a取3,b取2时
a取3,b取3时
∴P(方程有实数根)= .
.
点评:在与一元二次方程有关的求值问题中,必须满足下列条件:①二次项系数不为零;②在有的实数根的情况下必须满足△=b2-4ac≥0.用到的知识点为:概率=所求情况数与总情况数之比.
(2)根据(1)中所得出的a,b之间的关系,从a,b值中选取合适的值,再分析方程有实数根的概率.
解答:解:(1)∵方程有实数根
∴△≥0
∴(2
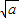 )2-4b≥0
)2-4b≥0∴4a-4b≥0
∴a-b≥0
∴当a-b≥0时,方程有实数根.
(2)由(1)可知:有以下几种可能方程有实数根
a取2,b取2时,
a取3,b取2时
a取3,b取3时
∴P(方程有实数根)=
 .
.点评:在与一元二次方程有关的求值问题中,必须满足下列条件:①二次项系数不为零;②在有的实数根的情况下必须满足△=b2-4ac≥0.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
(2009•扬州模拟)某私营玩具厂招工广告称:“本厂工人工作时间:每天工作8小时,每月工作25天;待遇:熟练工人按计件付工资,多劳多得,计件工资不少于1000元,每月另加福利工资100元,按月结算…”.该厂只生产两种玩具:小狗和小汽车,熟练工人晓凤一月份领工资1145元,她记录了如下一些数据:
(1)根据表格中的信息,试求出做1个小汽车所需时间和计件工资各是多少?
(2)设晓凤某月生产小狗x个,小汽车y个,月工资(计件工资+福利工资=月工资)为W元.试求W与x的函数关系式.(不需写出自变量x的取值范围)
(3)有一天,厂方从销量方面考虑,对生产作了调整:每个工人每月生产小狗的个数不少于生产小汽车个数的2倍,假设晓凤的工作效率不变,且服从厂家安排,请运用数学知识说明厂家招工广告是否有欺诈行为.
| 小狗件数(个) | 小汽车数(个) | 总时间(分钟) | 计件工资(元) |
| 1 | 1 | 35 | 2.8 |
| 2 | 2 | 70 | 5.6 |
| 3 | 2 | 85 | 6.6 |
(2)设晓凤某月生产小狗x个,小汽车y个,月工资(计件工资+福利工资=月工资)为W元.试求W与x的函数关系式.(不需写出自变量x的取值范围)
(3)有一天,厂方从销量方面考虑,对生产作了调整:每个工人每月生产小狗的个数不少于生产小汽车个数的2倍,假设晓凤的工作效率不变,且服从厂家安排,请运用数学知识说明厂家招工广告是否有欺诈行为.


 •sin60°+(-
•sin60°+(- )3•(
)3•( )-2.
)-2.