题目内容
(2009•扬州模拟)四个顶点都在正方形边上的四边形叫做正方形的内接四边形,如图1,正方形EFGH就是正方形ABCD的内接正方形,已知正方形ABCD的边长为a.(1)请在图1中画出面积最小的正方形ABCD的内接正方形E1F1G1H1(要求用文字标明取点方法);
(2)如图2,四边形E2F2G2H2是正方形ABCD的内接平行四边形,AE2=x,AH2=y,请探讨
①当x、y满足什么条件时,四边形E2F2G2H2是矩形;(要求写出过程)
②用x的代数式表示矩形E2F2G2H2的面积S,并写出S的取值范围.(直接写出结果)

【答案】分析:(1)分别取顺次连接正方形ABCD四边中点即可.
(2)首先证明△AE2H2≌△CG2F2推出CF2=AH2=y,然后证明△AE2H2∽△BF2E2,利用线段比求出,当四边形E2F2G2H2是矩形时,x,y满足的条件.分x=y,x+y=a两种情况考虑,得出S的取值范围.
解答:解:(1)分别取正方形ABCD四边中点,顺次连接(2分)(注:本题画图2分)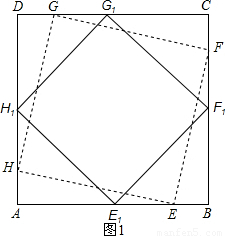
(2)①证明:△AE2H2≌△CG2F2,得CF2=AH2=y;(3分)
△AE2H2∽△BF2E2,得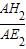 =
=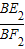 ,
,
即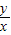 =
=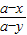 ,(2分)
,(2分)
化简得:(x-y)(x+y-a)=0,
∴x=y或x+y=a,(2分)
∴当x、y满足x=y或x+y=a时,四边形E2F2G2H2是矩形;(1分)
②当x=y时,S=-2x2+2ax(0<S≤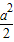 ).(2分)
).(2分)
当x+y=a时,S=2x2-2ax+a2(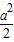 ≤S≤a2).(2分)
≤S≤a2).(2分)
点评:本题考查的是正方形的性质,相似三角形的判定以及全等三角形的判定的有关知识.
(2)首先证明△AE2H2≌△CG2F2推出CF2=AH2=y,然后证明△AE2H2∽△BF2E2,利用线段比求出,当四边形E2F2G2H2是矩形时,x,y满足的条件.分x=y,x+y=a两种情况考虑,得出S的取值范围.
解答:解:(1)分别取正方形ABCD四边中点,顺次连接(2分)(注:本题画图2分)

(2)①证明:△AE2H2≌△CG2F2,得CF2=AH2=y;(3分)
△AE2H2∽△BF2E2,得
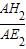 =
=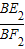 ,
,即
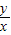 =
=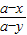 ,(2分)
,(2分)化简得:(x-y)(x+y-a)=0,
∴x=y或x+y=a,(2分)
∴当x、y满足x=y或x+y=a时,四边形E2F2G2H2是矩形;(1分)
②当x=y时,S=-2x2+2ax(0<S≤
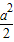 ).(2分)
).(2分)当x+y=a时,S=2x2-2ax+a2(
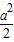 ≤S≤a2).(2分)
≤S≤a2).(2分)点评:本题考查的是正方形的性质,相似三角形的判定以及全等三角形的判定的有关知识.

练习册系列答案
相关题目
(2009•扬州模拟)某私营玩具厂招工广告称:“本厂工人工作时间:每天工作8小时,每月工作25天;待遇:熟练工人按计件付工资,多劳多得,计件工资不少于1000元,每月另加福利工资100元,按月结算…”.该厂只生产两种玩具:小狗和小汽车,熟练工人晓凤一月份领工资1145元,她记录了如下一些数据:
(1)根据表格中的信息,试求出做1个小汽车所需时间和计件工资各是多少?
(2)设晓凤某月生产小狗x个,小汽车y个,月工资(计件工资+福利工资=月工资)为W元.试求W与x的函数关系式.(不需写出自变量x的取值范围)
(3)有一天,厂方从销量方面考虑,对生产作了调整:每个工人每月生产小狗的个数不少于生产小汽车个数的2倍,假设晓凤的工作效率不变,且服从厂家安排,请运用数学知识说明厂家招工广告是否有欺诈行为.
| 小狗件数(个) | 小汽车数(个) | 总时间(分钟) | 计件工资(元) |
| 1 | 1 | 35 | 2.8 |
| 2 | 2 | 70 | 5.6 |
| 3 | 2 | 85 | 6.6 |
(2)设晓凤某月生产小狗x个,小汽车y个,月工资(计件工资+福利工资=月工资)为W元.试求W与x的函数关系式.(不需写出自变量x的取值范围)
(3)有一天,厂方从销量方面考虑,对生产作了调整:每个工人每月生产小狗的个数不少于生产小汽车个数的2倍,假设晓凤的工作效率不变,且服从厂家安排,请运用数学知识说明厂家招工广告是否有欺诈行为.

 x+b=0(a≥0).
x+b=0(a≥0). •sin60°+(-
•sin60°+(- )3•(
)3•( )-2.
)-2.