题目内容
 (2011•辽阳)如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为
(2011•辽阳)如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为| 3 |
| 3 |
分析:由已知的DE⊥AB,根据垂直的定义得到∠AED=90°,即三角形ADE为直角三角形,在此直角三角形中,根据锐角三角函数的定义得到sin∠BAD=
,将∠BAD的度数以及AD的值代入,利用特殊角的三角函数值,化简即可求出DE.
| DE |
| AD |
解答:解:∵DE⊥AB,
∴∠AED=90°,
在Rt△ADE中,∠BAD=60°,AD=2,
∴sin60°=
,
则DE=AD•sin60°=2×
=
.
故答案为:
∴∠AED=90°,
在Rt△ADE中,∠BAD=60°,AD=2,
∴sin60°=
| DE |
| AD |
则DE=AD•sin60°=2×
| ||
| 2 |
| 3 |
故答案为:
| 3 |
点评:此题考查了菱形的性质,直角三角形的性质,以及锐角三角函数,锐角三角函数很好的建立了三角形的边角关系,要求学生找出已知与未知的联系,选择合适的三角函数来解决问题.

练习册系列答案
相关题目
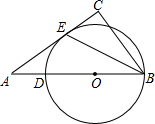 (2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(2011•辽阳)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.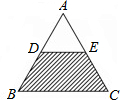 (2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( )
(2011•辽阳)如图,已知等边△ABC的面积为1,D、E分别为AB、AC的中点,若向图中随机抛掷一枚飞镖,飞镖落在阴影区域的概率是(不考虑落在线上的情形)( ) (2011•辽阳)如图,AB为⊙O直径,CD⊥AB,∠BDC=35°,则∠CAD=
(2011•辽阳)如图,AB为⊙O直径,CD⊥AB,∠BDC=35°,则∠CAD= 梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
梯形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.