题目内容
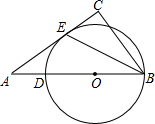（2011•辽阳）如图，⊙O经过点B、D、E，BD是⊙O的直径，∠C=90°，BE平分∠ABC．（1）试说明直线AC是⊙O的切线；
（2）当AE=4，AD=2时，求⊙O的半径及BC的长．
分析：（1）连接OE，证明出∠AEO=90°，即可说明直线AC是⊙O的切线；
（2）知道OE∥BC，利用平行线分线段成比例定理即可解答．
（2）知道OE∥BC，利用平行线分线段成比例定理即可解答．
解答：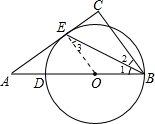
（1）证明：连接OE．
∵BE是∠ABC的平分线，
∴∠1=∠2．
∵OE=OB，
∴∠1=∠3．
∴∠2=∠3．
∴OE∥BC．
又∠C=90°，
∴∠AEO=90°．
∴AC是⊙O的切线．
（2）解：设⊙O的半径为r，在Rt△AEO中，由勾股定理可得OA2=OE2+AE2．
∵AE=4，AD=2，
∴（2+r）2=r2+42．
∴r=3．
∵OE∥BC，
∴
=
．
∴
=
．
∴BC=
．
（1）证明：连接OE．∵BE是∠ABC的平分线，
∴∠1=∠2．
∵OE=OB，
∴∠1=∠3．
∴∠2=∠3．
∴OE∥BC．
又∠C=90°，
∴∠AEO=90°．
∴AC是⊙O的切线．
（2）解：设⊙O的半径为r，在Rt△AEO中，由勾股定理可得OA2=OE2+AE2．
∵AE=4，AD=2，
∴（2+r）2=r2+42．
∴r=3．
∵OE∥BC，
∴
| AO |
| AB |
| OE |
| BC |
∴
| 2+3 |
| 2+6 |
| 3 |
| BC |
∴BC=
| 24 |
| 5 |
点评：本题考查了切线的判定、勾股定理和平行线分线段成比例定理，是一道综合题，但难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
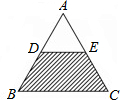（2011•辽阳）如图，已知等边△ABC的面积为1，D、E分别为AB、AC的中点，若向图中随机抛掷一枚飞镖，飞镖落在阴影区域的概率是（不考虑落在线上的情形）（ ）
（2011•辽阳）如图，AB为⊙O直径，CD⊥AB，∠BDC=35°，则∠CAD=
（2011•辽阳）如图，已知菱形ABCD的边长为2，∠BAD=60°，若DE⊥AB，垂足为点E，则DE的长为
梯形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．