ЬтФПФкШн
ЃЈ2011•СЩбєЃЉШчЭМЃЌвбжЊRtЁїABOЃЌЁЯBAO=90ЁуЃЌвдЕуOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊyжсЃЌНЈСЂЦНУцжБНЧзјБъЯЕЃЌAO=3ЃЌЁЯAOB=30ЁуЃЌНЋRtЁїABOбиOBЗелКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуDДІЃЎ
ЃЈ1ЃЉЧѓDЕузјБъЃЛ
ЃЈ2ЃЉШєХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§BЁЂDСНЕуЃЌЧѓДЫХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖЅЕуЮЊEЃЌЫќЕФЖдГЦжсгыOBНЛгкЕуFЃЌЕуPЮЊЩфЯпOBЩЯвЛЖЏЕуЃЌЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуMЃЎЪЧЗёДцдкЕуPЃЌЪЙЕУвдEЁЂFЁЂMЁЂPЮЊЖЅЕуЕФЫФБпаЮЮЊЕШбќ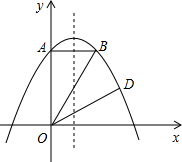 ЬнаЮЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЬнаЮЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВЮПМЙЋЪНЃКХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖЅЕузјБъЪЧЃЈ-
ЃЌ
ЃЉЃЎ
ЃЈ1ЃЉЧѓDЕузјБъЃЛ
ЃЈ2ЃЉШєХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§BЁЂDСНЕуЃЌЧѓДЫХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖЅЕуЮЊEЃЌЫќЕФЖдГЦжсгыOBНЛгкЕуFЃЌЕуPЮЊЩфЯпOBЩЯвЛЖЏЕуЃЌЙ§ЕуPзїyжсЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуMЃЎЪЧЗёДцдкЕуPЃЌЪЙЕУвдEЁЂFЁЂMЁЂPЮЊЖЅЕуЕФЫФБпаЮЮЊЕШбќ
 ЬнаЮЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЬнаЮЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎВЮПМЙЋЪНЃКХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖЅЕузјБъЪЧЃЈ-
| b |
| 2a |
| 4ac-b2 |
| 4a |
ЗжЮіЃКЃЈ1ЃЉЙ§ЕуDзїDCЁЭxжсгкЕуEЃЌШчЭМЃЈ1ЃЉЃЌгЩжсЖдГЦЕУГіOD=3ЃЌЁЯDOE=30ЁуЃЌЙЪПЩвдЧѓГіDEЕФжЕЃЌгЩЙДЙЩЖЈРэОЭПЩвдЧѓГіOEЕФжЕЃЌДгЖјПЩвдЧѓГіDЕФзјБъЃЎ
ЃЈ2ЃЉЭЈЙ§НтжБНЧШ§НЧаЮAOBЧѓГіABЕФжЕЃЌЧѓГіЕуBЕФзјБъЃЌдйНЋBЁЂDЕФзјБъДњШыНтЮіЪНОЭПЩвдЧѓГіХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ3ЃЉРћгУЃЈ2ЃЉЕФНтЮіЪНЃЌЧѓГіEЕуЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпOBЕФНтЮіЪНЃЌДгЖјЧѓГіFЕФзјБъЃЌДгЖјЧѓГіEFЃЌЩшPЃЈxЃЌyЃЉЃЌзїEHЁЭPMгкЕуHЃЌFGЁЭPMгкЕуGЃЌШчЭМЃЈ2ЃЉЃЌгЩЬтвтПЩЕУPH=GMДгЖјЧѓГіЕуPЕФзјБъЃЎ
ЃЈ2ЃЉЭЈЙ§НтжБНЧШ§НЧаЮAOBЧѓГіABЕФжЕЃЌЧѓГіЕуBЕФзјБъЃЌдйНЋBЁЂDЕФзјБъДњШыНтЮіЪНОЭПЩвдЧѓГіХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ3ЃЉРћгУЃЈ2ЃЉЕФНтЮіЪНЃЌЧѓГіEЕуЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпOBЕФНтЮіЪНЃЌДгЖјЧѓГіFЕФзјБъЃЌДгЖјЧѓГіEFЃЌЩшPЃЈxЃЌyЃЉЃЌзїEHЁЭPMгкЕуHЃЌFGЁЭPMгкЕуGЃЌШчЭМЃЈ2ЃЉЃЌгЩЬтвтПЩЕУPH=GMДгЖјЧѓГіЕуPЕФзјБъЃЎ
НтД№ЃК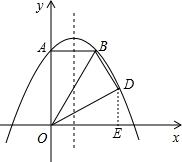 НтЃКЃЈ1ЃЉЙ§ЕуDзїDEЁЭxжсгкЕуEЃЌШчЭМЃЈ1ЃЉЃЎ
НтЃКЃЈ1ЃЉЙ§ЕуDзїDEЁЭxжсгкЕуEЃЌШчЭМЃЈ1ЃЉЃЎ
гЩЗелПЩжЊЃКDO=AO=3ЃЌ
ЁЯAOB=ЁЯBOD=30ЁуЃЌ
ЁрЁЯDOE=30ЁуЃЎ
ЁрDE=
дкRtЁїCODжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
OE=
ЁрDЃЈ
ЃЌ
ЃЉ
ЃЈ2ЃЉдкRtЁїAOBжаЃЌ
AB=AO•tan30Ёу=3ЁС
=
ЃЌ
ЁрBЃЈ
ЃЌ3ЃЉЃЎ
ЁпХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§BЃЈ
ЃЌ3ЃЉЃЌDЃЈ
ЃЌ
ЃЉСНЕуЃЌ
Ёр
НтЕУ
ЁрДЫХзЮяЯпБэДяЪНЮЊy=-
x2+
x+3ЃЎ
ЃЈ3ЃЉДцдкЗћКЯЬѕМўЕФЕуPЃЌЩшPЃЈxЃЌyЃЉЃЌ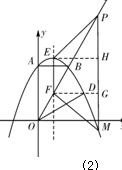
зїEHЁЭPMгкЕуHЃЌFGЁЭPMгкЕуGЃЌШчЭМЃЈ2ЃЉЃЎ
ЁпEЮЊХзЮяЯпy=-
x2+
x+3ЕФЖЅЕуЃЌ
ЁрEЃЈ
ЃЌ
ЃЉЃЎ
ЩшOBЫљдкжБЯпЕФБэДяЪНЮЊy=kxЃЌ
НЋЕуBЃЈ
ЃЌ3ЃЉДњШыЃЌЕУk=
ЃЌ
Ёрy=
xЃЎ
ЁпPдкЩфЯпOBЩЯЃЌ
ЁрPЃЈxЃЌ
xЃЉЃЌFЃЈ
ЃЌ
ЃЉЃЎ
дђHЃЈxЃЌ
ЃЉGЃЈxЃЌ
ЃЉЃЎ
ЁпMдкХзЮяЯпЩЯЃЌMЃЈxЃЌ-
x2+
x+3ЃЉЃЎ
вЊЪЙЫФБпаЮEFMPЮЊЕШбќЬнаЮЃЌжЛашPH=GMЃЎ
x-
=
-ЃЈ-
x2+
x+3ЃЉЃЌ
МД-
x2+
x+3+
x=5ЃЎ
НтЕУx1=2
ЃЌx2=
ЃЎ
ЁрP1ЕузјБъЮЊЃЈ2
ЃЌ6ЃЉЃЌP2ЕузјБъЮЊЃЈ
ЃЌ
ЃЉгыFжиКЯЃЌгІЩсШЅЃЎ
ЁрPЕузјБъЮЊЃЈ2
ЃЌ6ЃЉЃЎ
 НтЃКЃЈ1ЃЉЙ§ЕуDзїDEЁЭxжсгкЕуEЃЌШчЭМЃЈ1ЃЉЃЎ
НтЃКЃЈ1ЃЉЙ§ЕуDзїDEЁЭxжсгкЕуEЃЌШчЭМЃЈ1ЃЉЃЎгЩЗелПЩжЊЃКDO=AO=3ЃЌ
ЁЯAOB=ЁЯBOD=30ЁуЃЌ
ЁрЁЯDOE=30ЁуЃЎ
ЁрDE=
| 3 |
| 2 |
дкRtЁїCODжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
OE=
3
| ||
| 2 |
ЁрDЃЈ
3
| ||
| 2 |
| 3 |
| 2 |
ЃЈ2ЃЉдкRtЁїAOBжаЃЌ
AB=AO•tan30Ёу=3ЁС
| ||
| 3 |
| 3 |
ЁрBЃЈ
| 3 |
ЁпХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§BЃЈ
| 3 |
3
| ||
| 2 |
| 3 |
| 2 |
Ёр
|
НтЕУ
|
ЁрДЫХзЮяЯпБэДяЪНЮЊy=-
| 2 |
| 3 |
2
| ||
| 3 |
ЃЈ3ЃЉДцдкЗћКЯЬѕМўЕФЕуPЃЌЩшPЃЈxЃЌyЃЉЃЌ

зїEHЁЭPMгкЕуHЃЌFGЁЭPMгкЕуGЃЌШчЭМЃЈ2ЃЉЃЎ
ЁпEЮЊХзЮяЯпy=-
| 2 |
| 3 |
2
| ||
| 3 |
ЁрEЃЈ
| ||
| 2 |
| 7 |
| 2 |
ЩшOBЫљдкжБЯпЕФБэДяЪНЮЊy=kxЃЌ
НЋЕуBЃЈ
| 3 |
| 3 |
Ёрy=
| 3 |
ЁпPдкЩфЯпOBЩЯЃЌ
ЁрPЃЈxЃЌ
| 3 |
| ||
| 2 |
| 3 |
| 2 |
дђHЃЈxЃЌ
| 7 |
| 2 |
| 3 |
| 2 |
ЁпMдкХзЮяЯпЩЯЃЌMЃЈxЃЌ-
| 2 |
| 3 |
2
| ||
| 3 |
вЊЪЙЫФБпаЮEFMPЮЊЕШбќЬнаЮЃЌжЛашPH=GMЃЎ
| 3 |
| 7 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
2
| ||
| 3 |
МД-
| 2 |
| 3 |
2
| ||
| 3 |
| 3 |
НтЕУx1=2
| 3 |
| ||
| 2 |
ЁрP1ЕузјБъЮЊЃЈ2
| 3 |
| ||
| 2 |
| 3 |
| 2 |
ЁрPЕузјБъЮЊЃЈ2
| 3 |
ЕуЦРЃКБОЬтЪЧвЛЕРЖўДЮКЏЪ§ЕФзлКЯЪдЬтЃЌПМВщСЫЕуЕФзјБъЃЌД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§ЕФНтЮіЪНЃЌЕШбќЬнаЮЕФХаЖЈМАаджЪМАНтжБНЧШ§НЧаЮЕФдЫгУЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
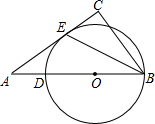 ЃЈ2011•СЩбєЃЉШчЭМЃЌЁбOОЙ§ЕуBЁЂDЁЂEЃЌBDЪЧЁбOЕФжБОЖЃЌЁЯC=90ЁуЃЌBEЦНЗжЁЯABCЃЎ
ЃЈ2011•СЩбєЃЉШчЭМЃЌЁбOОЙ§ЕуBЁЂDЁЂEЃЌBDЪЧЁбOЕФжБОЖЃЌЁЯC=90ЁуЃЌBEЦНЗжЁЯABCЃЎ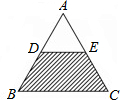 ЃЈ2011•СЩбєЃЉШчЭМЃЌвбжЊЕШБпЁїABCЕФУцЛ§ЮЊ1ЃЌDЁЂEЗжБ№ЮЊABЁЂACЕФжаЕуЃЌШєЯђЭМжаЫцЛњХзжРвЛУЖЗЩякЃЌЗЩякТфдквѕгАЧјгђЕФИХТЪЪЧЃЈВЛПМТЧТфдкЯпЩЯЕФЧщаЮЃЉЃЈЁЁЁЁЃЉ
ЃЈ2011•СЩбєЃЉШчЭМЃЌвбжЊЕШБпЁїABCЕФУцЛ§ЮЊ1ЃЌDЁЂEЗжБ№ЮЊABЁЂACЕФжаЕуЃЌШєЯђЭМжаЫцЛњХзжРвЛУЖЗЩякЃЌЗЩякТфдквѕгАЧјгђЕФИХТЪЪЧЃЈВЛПМТЧТфдкЯпЩЯЕФЧщаЮЃЉЃЈЁЁЁЁЃЉ ЃЈ2011•СЩбєЃЉШчЭМЃЌABЮЊЁбOжБОЖЃЌCDЁЭABЃЌЁЯBDC=35ЁуЃЌдђЁЯCAD=
ЃЈ2011•СЩбєЃЉШчЭМЃЌABЮЊЁбOжБОЖЃЌCDЁЭABЃЌЁЯBDC=35ЁуЃЌдђЁЯCAD= ЃЈ2011•СЩбєЃЉШчЭМЃЌвбжЊСтаЮABCDЕФБпГЄЮЊ2ЃЌЁЯBAD=60ЁуЃЌШєDEЁЭABЃЌДЙзуЮЊЕуEЃЌдђDEЕФГЄЮЊ
ЃЈ2011•СЩбєЃЉШчЭМЃЌвбжЊСтаЮABCDЕФБпГЄЮЊ2ЃЌЁЯBAD=60ЁуЃЌШєDEЁЭABЃЌДЙзуЮЊЕуEЃЌдђDEЕФГЄЮЊ