Question

已知：如图，AC⊙O是的直径，BC是⊙O的弦，点P是⊙O外一点，∠PBA=∠C．

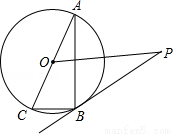
（1）求证：PB是⊙O的切线；

（2）若OP∥BC，且OP=8，BC=2．求⊙O的半径．

 

Answer 1

【答案】

解：（1）证明：连接OB，

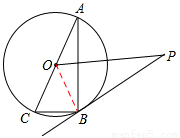
∵AC是⊙O直径，∴∠ABC=90°。

∵OC=OB，∴∠OBC=∠ACB。

∵∠PBA=∠ACB，∴∠PBA=∠OBC。

∴∠PBA+∠OBA=∠OBC+∠ABO=∠ABC=90°。

∴OB⊥PB。

∵OB为半径，∴PB是⊙O的切线。

（2）设⊙O的半径为r，则AC=2r，OB=R，

∵OP∥BC，∠OBC=∠OCB，∴∠POB=∠OBC=∠OCB。

∵∠PBO=∠ABC=90°，∴△PBO∽△ABC。

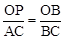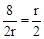∴，即，解得。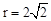

∴⊙O的半径为。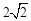

【解析】

试题分析：（1）连接OB，求出∠ABC=90°，∠PBA=∠OBC=∠OCB，推出∠PBO=90°，根据切线的判定推出即可。

 （2）证△PBO和△ABC相似，得出比例式，代入求出即可。