题目内容
已知:如图,AC是⊙O的直径,AB和⊙O相交于E,BC和⊙O相切于C,D在BC上,DE是⊙O的切线,E 是切点,
是切点,求证:(1)OD∥AB;
(2)2DE2=BE•OD;
(3)设BE=2,∠ODE=a,则cos2a=
| 1 | OD |
分析:(1)连接CE,可证OD⊥CE,由AC是直径,可证AE⊥CE,则OD∥AB;
(2)先证明Rt△BCE∽Rt△DOE,得出BC:OD=BE:DE,根据DE是Rt△BCE斜边上的中线,故BC=2DE,则而DE是Rt△BCE斜边上的中线,故BC=2DE;
(3)可知DB=DE,得到∠DEB=∠DBE=α,则cosa=
,由(2)得DE2=OD,即cos2a=
.
(2)先证明Rt△BCE∽Rt△DOE,得出BC:OD=BE:DE,根据DE是Rt△BCE斜边上的中线,故BC=2DE,则而DE是Rt△BCE斜边上的中线,故BC=2DE;
(3)可知DB=DE,得到∠DEB=∠DBE=α,则cosa=
| 1 |
| DE |
| 1 |
| OD |
解答: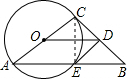 (1)证明:连接CE,∵DC和DE都与⊙O相切,
(1)证明:连接CE,∵DC和DE都与⊙O相切,
∴DC=DE,∠CDO=∠EDO,
∴OD⊥CE.(1分)
又AC是直径,故∠CEA=90°,
即AE⊥CE,
∴OD∥AB;(2分)
(2)证明:
证法一:DE、DC是⊙O的切线,OD∥AB,故∠ODE=∠ODC=∠B.(3分)
∴Rt△BCE∽Rt△DOE,
∴BC:OD=BE:DE,
即BC•DE=OD•BE.(5分)
而DE是Rt△BCE斜边上的中线,故BC=2DE,
∴2DE2=BE•OD.(6分)
证法二:BC2=BE•BA,OD是△ABC的中位线,(3分)
∴BA=2OD,又BC=2DE,
∴4DE2=BE•2OD,
∴2DE2=BE•OD.(6分)
(3)解:
解法一:由②和已知条件得DE2=OD,即OD2-OE2=OD.(7分)
两边同除以OD2得1-(
)2-
,
得1-sin2a=
,
∴cos2a=
(8分)
解法二:注意到D是BC的中点,可知DB=DE,
∴∠DEB=∠DBE=α,于是cosa=
(过D作DG⊥EB可知).(7分)
由(2)及已知可得DE2=OD,
∴cos2a=
.(8分)
 (1)证明:连接CE,∵DC和DE都与⊙O相切,
(1)证明:连接CE,∵DC和DE都与⊙O相切,∴DC=DE,∠CDO=∠EDO,
∴OD⊥CE.(1分)
又AC是直径,故∠CEA=90°,
即AE⊥CE,
∴OD∥AB;(2分)
(2)证明:
证法一:DE、DC是⊙O的切线,OD∥AB,故∠ODE=∠ODC=∠B.(3分)
∴Rt△BCE∽Rt△DOE,
∴BC:OD=BE:DE,
即BC•DE=OD•BE.(5分)
而DE是Rt△BCE斜边上的中线,故BC=2DE,
∴2DE2=BE•OD.(6分)
证法二:BC2=BE•BA,OD是△ABC的中位线,(3分)
∴BA=2OD,又BC=2DE,
∴4DE2=BE•2OD,
∴2DE2=BE•OD.(6分)
(3)解:
解法一:由②和已知条件得DE2=OD,即OD2-OE2=OD.(7分)
两边同除以OD2得1-(
| OE |
| OD |
| 1 |
| OD |
得1-sin2a=
| 1 |
| OD |
∴cos2a=
| 1 |
| OD |
解法二:注意到D是BC的中点,可知DB=DE,
∴∠DEB=∠DBE=α,于是cosa=
| 1 |
| DE |
由(2)及已知可得DE2=OD,
∴cos2a=
| 1 |
| OD |
点评:本题考查的是三角形的中位线定理,切线的性质定理,勾股定理.

练习册系列答案
相关题目
 已知:如图,AC是∠BAD和∠BCD的角平分线,则△ABC≌△ADC用( )判定.
已知:如图,AC是∠BAD和∠BCD的角平分线,则△ABC≌△ADC用( )判定.| A、AAA | B、ASA或AAS | C、SSS | D、SAS |
 21、已知:如图,AC是?ABCD的对角线,MN∥AC,分别交AD、CD于点P、Q,试说明MP=QN.
21、已知:如图,AC是?ABCD的对角线,MN∥AC,分别交AD、CD于点P、Q,试说明MP=QN. 已知:如图,AC是⊙O的直径,AB是弦,MN是过点A的直线,AB等于半径长.
已知:如图,AC是⊙O的直径,AB是弦,MN是过点A的直线,AB等于半径长.
 16、如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②作AE⊥BC于点E,AF⊥DC于点F.从中任选一个作为条件,证明BE=DF.
16、如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②作AE⊥BC于点E,AF⊥DC于点F.从中任选一个作为条件,证明BE=DF. (2013•昆明)已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.
(2013•昆明)已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.