题目内容
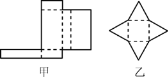
【题目】如图1, O为正方形ABCD的中心,分别延长OA,OD到点F,E,使OF=2OA,OE=2OD,连接EF,将△FOE绕点O按逆时针方向旋转角α得到△FOE,连接AE,BF(如图2).
(1)探究AE与BF的数量关系,并给予证明;
(2)当α=30°时,求证: △AOE为直角三角形.

【答案】(1)AE=BF,理由见解析;(2)证明见解析.
【解析】试题分析:(1)利用旋转不变量找到相等的角和线段,证得△E′AO≌△F′BO后即可证得结论;
(2)利用已知角,得出∠GAE′=∠GE′A=30°,从而证明直角三角形.
试题解析:(1)证明:∵O为正方形ABCD的中心,
∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E′OF′,
∴OE′=OF′,
∵∠F′OB=∠E′OA,OA=OB,
在△E′AO和△F′BO中,
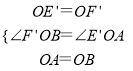 ,
,
∴△E′AO≌△F′BO,
∴AE′=BF′;
(2)证明:∵取OE′中点G,连接AG,
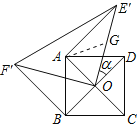
∵∠AOD=90°,α=30°,
∴∠E′OA=90°-α=60°,
∵OE′=2OA,
∴OA=OG,
∴∠E′OA=∠AGO=∠OAG=60°,
∴AG=GE′,
∴∠GAE′=∠GE′A=30°,
∴∠E′AO=90°,
∴△AOE′为直角三角形.

【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |

(1)频数分布表中的m= , n=;
(2)样本中位数所在成绩的级别是 , 扇形统计图中,E组所对应的扇形圆心角的度数是;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?