题目内容
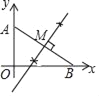
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=![]() ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,直接写出以点O、M、B为其中三个顶点的平行四边形的第四个顶点P的坐标

【答案】(1)详见解析;(2)(2,![]() );(3)P(6,1.5)或P(﹣2,1.5)或P(2,﹣1.5)
);(3)P(6,1.5)或P(﹣2,1.5)或P(2,﹣1.5)
【解析】
(1)直接利用线段垂直平分线的作法结合直角三角形的性质得出答案;
(2)利用勾股定理得出OB的长,再利用M点为AB的中点即可得出其坐标.
(3)根据平行四边形的性质直接得出P的坐标即可.
(1)如图所示:点M,即为所求;
(2)∵sin∠OAB=![]() ,
,
∴设OB=4x,AB=5x,
由勾股定理可得:32+(4x)2=(5x)2,
解得:x=1,
由作图可得:M为AB的中点,则M的坐标为:(2,![]() ).
).
(3)∵B(4,0),M(2,![]() ),OMBP是平行四边形,
),OMBP是平行四边形,
∴MP∥x轴,
∴P的纵坐标为1.5,MP=4,
可得:P(6,1.5)或P(﹣2,1.5),
∵当OP∥MB时,
∴P(2,﹣1.5),
综上所述:P(6,1.5)或P(﹣2,1.5)或P(2,﹣1.5),

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目