题目内容
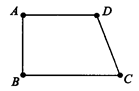
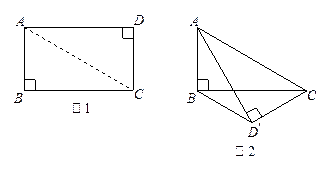 如图1,矩形纸片ABCD中,AB=4,BC=4
如图1,矩形纸片ABCD中,AB=4,BC=4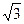 ,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.解:设AD’交BC于O,
方法一:
过点B作BE⊥AD’于E,
矩形ABCD中,
∵AD∥BC,AD=BC,
∠B=∠D=∠BAD=90°,
在Rt△ABC中,
∵tan∠BAC=
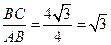 ,
,∴∠BAC=60°,∴∠DAC=90°—∠BAC=30°,……………………………2分
∵将△ACD沿对角线AC向下翻折,得到△ACD’,
∴AD’=AD=BC=
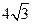 ,∠1=∠DAC=30°,
,∠1=∠DAC=30°,∴∠4=∠BAC—∠1=30°,
又在Rt△ABE中,∠AEB=90°,∴BE=2, ……………………………………4分
∴AE=
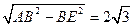 ,∴D’E=AD’—AE=
,∴D’E=AD’—AE=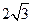 ,
,∴AE=D’E,即BE垂直平分AD’,∴BD’=AB=4. ……………………………5分
方法二:
矩形ABCD中,∵AD∥BC,AD=BC,∠B=∠D=90°,∴∠ACB=∠DAC,
在Rt△ABC中,∵tan∠BAC=
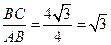 ,
,∴∠BAC=60°,∴∠ACB=90°—∠BAC=30°,……………………………2分∵将△ACD沿对角线AC向下翻折,得到△ACD’,
∴AD=AD’=BC,∠1=∠DAC=∠ACB=30°,
∴OA=OC,
∴OD’=OB,∴∠2=∠3,
∵∠BOA=∠1+∠ACB=60°, ∠2+∠3=∠BOA,
∴∠2=
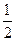 ∠BOA=30°,…………………………………………………………4分
∠BOA=30°,…………………………………………………………4分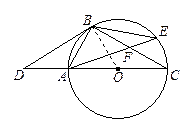 ∵∠4=∠BAC—∠1=30°,∴∠2=∠4,∴BD’=AB=4.
∵∠4=∠BAC—∠1=30°,∴∠2=∠4,∴BD’=AB=4. 略

练习册系列答案
相关题目
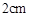 ,面积是
,面积是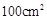 ,则这个长方形的周长为
,则这个长方形的周长为 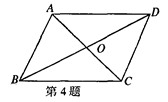

 中,
中, ,
, ,
,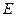 为
为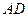 中点,连接
中点,连接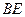 ,
,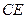 .
.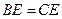 ;
;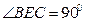 ,过点
,过点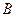 作
作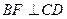 ,垂足为点
,垂足为点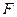 ,交
,交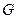 ,连接
,连接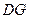 .
.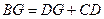 .
.
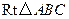 中,
中,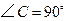 ,
,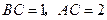 ,把边长分别为
,把边长分别为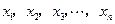 的
的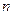 个正方形依次放入
个正方形依次放入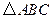 中,请回答下列问题:
中,请回答下列问题: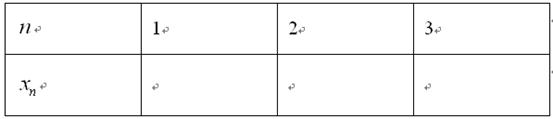
 ;
;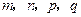 是正整数,且
是正整数,且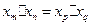 ,试判断
,试判断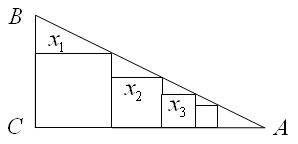
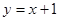 与y轴交于点
与y轴交于点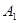 ,以
,以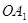 为边作正方形
为边作正方形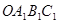 然后延长
然后延长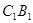 与直线
与直线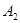 ,得到第一个梯形
,得到第一个梯形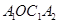 ;再以
;再以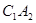 为边作正方形
为边作正方形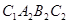 ,同样延长
,同样延长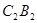 与直线
与直线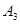 得到第二个梯形
得到第二个梯形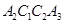 ;,再以
;,再以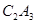 为边作正方形
为边作正方形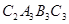 ,延长
,延长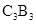 ,得到第三个梯形;……则第2个
,得到第三个梯形;……则第2个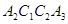
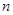 (n是正整数)个梯形的面积是 (用含n的式子
(n是正整数)个梯形的面积是 (用含n的式子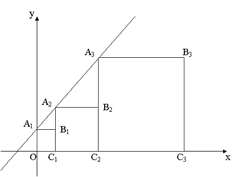
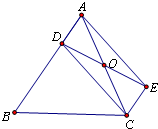
 泸州,21,5分)如图,已知D是△ABC的边AB上一点,CE∥AB,DE交
泸州,21,5分)如图,已知D是△ABC的边AB上一点,CE∥AB,DE交 AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.