题目内容
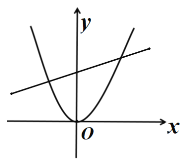
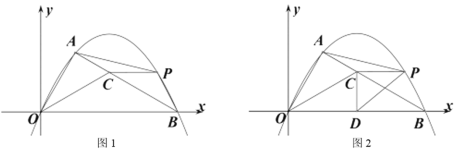
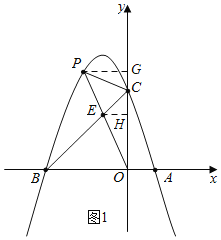
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2x+c与x轴交于点A(1,0),点B(﹣3,0),与y轴交于点C,连接BC,点P在第二象限的抛物线上,连接PC、PO,线段PO交线段BC于点 E.
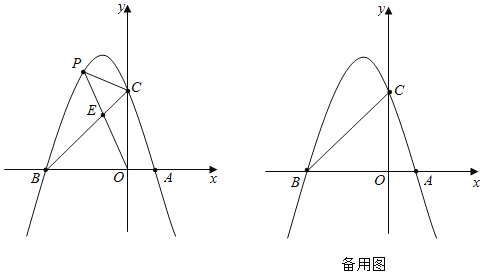
(1)求抛物线的表达式;
(2)若△PCE的面积为S1,△OCE的面积为S2,当![]() =
=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)已知点C关于抛物线对称轴的对称点为点N,连接BN,点H在x轴上,当∠HCB=∠NBC时,
①求满足条件的所有点H的坐标;
②当点H在线段AB上时,点Q是线段BH外一点,QH=1,连接BQ,将线段BQ绕着点Q顺时针旋转90°,得到线段QM,连接MH,直接写出线段MH的取值范围.
【答案】(1)y=﹣x2﹣2x+3;(2)点P的坐标是(﹣2,3)或(﹣1,4);(3)①点H的坐标是(﹣1,0)或(﹣9,0);②2﹣![]() ≤MH≤2+
≤MH≤2+![]() .
.
【解析】
(1)先把点A(1,0),点B(﹣3,0)代入抛物线y=ax2﹣2x+c中列方程组,解方程组可得a和c的值,从而得抛物线的表达式;
(2)先根据待定系数法求BC的解析式为:y=x+3,根据同高三角形面积的比等于对应底边的比,可得![]() ,证明△OEH∽△OPG,得
,证明△OEH∽△OPG,得![]() ,可设E(3m,3m+3),则P(5m,﹣25m2﹣10m+3),代入比例式可得方程,解出即可得结论;
,可设E(3m,3m+3),则P(5m,﹣25m2﹣10m+3),代入比例式可得方程,解出即可得结论;
(3)①由对称得:N(﹣2,3),有两种情况:如图2,i)当BN∥CH1时,∠H1CB=∠NBC,根据平移的性质可得点H1的坐标;ii)当∠H2CB=∠NBC,设H2(n,0),直线CH2与BN交于点M,确定BN和CH2的解析式,利用方程组的解可得M的坐标(![]() ,
,![]() ),根据两点的距离公式利用BM=CM,列方程可得结论;
),根据两点的距离公式利用BM=CM,列方程可得结论;
②如图3,当Q在x轴下方时,且MH⊥x轴时,MH最小,作辅助线,构建矩形MFGH是,证明△BGQ≌△QFM(AAS),得GQ=GH=FM,可得△QHG是等腰直角三角形,由斜边为1可得QG=GH=![]() ,利用全等三角形的性质与线段和与差可得结论;同理如图4,当Q在x轴上方时,且MH⊥x轴时,MH最大,同理可得最大值MH的长,从而得结论.
,利用全等三角形的性质与线段和与差可得结论;同理如图4,当Q在x轴上方时,且MH⊥x轴时,MH最大,同理可得最大值MH的长,从而得结论.
(1)把点A(1,0),点B(﹣3,0)代入抛物线y=ax2﹣2x+c中,
得:![]() ,
,
解得:![]() ,
,
∴抛物线的表达式为:y=﹣x2﹣2x+3;
(2)如图1,过P作PG⊥y轴于G,过E作EH⊥y轴于H,
当x=0时,y=3,
∴C(0,3),
设BC的解析式为:y=kx+b,
则![]() ,解得
,解得![]() ,
,
∴BC的解析式为:y=x+3,
∵△PCE的面积为S1,△OCE的面积为S2,且![]() ,
,
∴![]() ,
,
∵EH∥PG,
∴△OEH∽△OPG,
∴![]() ,
,
∴设E(3m,3m+3),则P(5m,﹣25m2﹣10m+3),
∴![]() ,
,
∴25m2+15m+2=0,
(5m+2)(5m+1)=0,
m1=![]() ,m2=
,m2=![]() ,
,
当m=![]() 时,5m=﹣2,则P(﹣2,3),
时,5m=﹣2,则P(﹣2,3),
当m=![]() 时,5m=﹣1,则P(﹣1,4),
时,5m=﹣1,则P(﹣1,4),
综上,点P的坐标是(﹣2,3)或(﹣1,4);
(3)①由对称得:N(﹣2,3),
∵∠HCB=∠NBC,

如图2,连接CN,有两种情况:
i)当BN∥CH1时,∠H1CB=∠NBC,
∵CN∥AB,
∴四边形CNBH1是平行四边形,
∴![]() ,
,
∴H1(﹣1,0);
ii)当∠H2CB=∠NBC,
设H2(n,0),直线CH2与BN交于点M,
∴BM=CM,
∵B(﹣3,0),N(﹣2,3),
∴同理可得BN的解析式为:y=3x+9,
设CH2的解析式为:y=k1x+b1,
则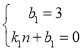 ,解得:
,解得: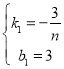 ,
,
∴设CH2的解析式为:y=![]() +3,
+3,
解方程组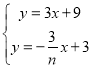 ,得
,得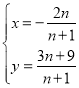 ,
,
∴M(![]() ,
,![]() ),
),
∵BM=CM,
∴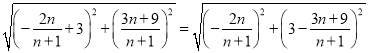 ,
,
解得:n=﹣9或﹣1(舍),
∴H2(﹣9,0),
综上,点H的坐标是(﹣1,0)或(﹣9,0);
②如图3,当Q在x轴下方时,且MH⊥x轴时,MH最小,过Q作QG⊥x轴,过M作MF⊥QG于F,则四边形MFGH是矩形,
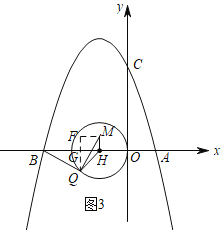
∴FM=GH,FG=MH,
∵∠BQM=∠F=90°,
∴∠BQG+∠GQM=∠FMQ+∠GQM=90°,
∴∠BQG=∠FMQ,
∵BQ=QM,∠BGQ=∠F=90°,
∴△BGQ≌△QFM(AAS),
∴FM=GQ,BG=FQ,
∴GQ=FM=GH,
∵QH=1,
∴QG=GH=![]() ,
,
∴MH=FG=FQ﹣QG=BG﹣GH=2﹣![]() ﹣
﹣![]() =2﹣
=2﹣![]() ;
;
如图4,当Q在x轴上方时,且MH⊥x轴时,MH最大,过Q作QG⊥x轴,作QF⊥MH于F,则四边形QFHG是矩形,
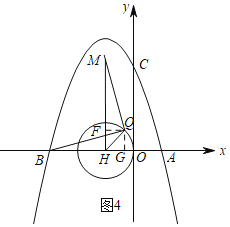
∴FQ=GH,GQ=FH,
同理得△BGQ≌△MFQ(AAS),
∴QG=FQ=GH,BG=MF,
∵QH=1,
∴QG=GH=![]() ,
,
∴MH=FM+FH=BG+GH=2+![]() +
+![]() =2+
=2+![]() ;
;
∴MH的取值范围是2﹣![]() ≤MH≤2+
≤MH≤2+![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
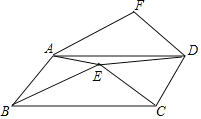
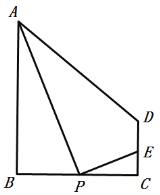
小学生10分钟应用题系列答案【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .P为线段
.P为线段![]() 上的一动点,且和B、C不重合,连接
上的一动点,且和B、C不重合,连接![]() ,过点P作
,过点P作![]() 交射线
交射线![]() 于点E.
于点E.
聪聪根据学习函数的经验,对这个问题进行了研究:
(1)通过推理,他发现![]() ,请你帮他完成证明.
,请你帮他完成证明.
(2)利用几何画板,他改变![]() 的长度,运动点P,得到不同位置时,
的长度,运动点P,得到不同位置时,![]() 、
、![]() 的长度的对应值:
的长度的对应值:
当![]() 时,得表1:
时,得表1:
| … | 1 | 2 | 3 | 4 | 5 | … |
| … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
当![]() 时,得表2:
时,得表2:
| … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
这说明,点P在线段![]() 上运动时,要保证点E总在线段
上运动时,要保证点E总在线段![]() 上,
上,![]() 的长度应有一定的限制.
的长度应有一定的限制.
①填空:根据函数的定义,我们可以确定,在![]() 和
和![]() 的长度这两个变量中,_____的长度为自变量,_____的长度为因变量;
的长度这两个变量中,_____的长度为自变量,_____的长度为因变量;
②设![]() ,当点P在线段
,当点P在线段![]() 上运动时,点E总在线段
上运动时,点E总在线段![]() 上,求m的取值范围.
上,求m的取值范围.