题目内容
【题目】如图,∠AOB=90°,OA=12cm,OB=8cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,并且它们的运动时间也相等.
(1)请用直尺和圆规作出C处的位置,不必叙述作图过程,保留作图痕迹;
(2)求线段OC的长.

【答案】(1)详见解析;(2)![]() cm.
cm.
【解析】
(1)作AB的垂直平分线,交OA于点C,则点C即为所求;
(2)设BC=xcm,根据题意用x表示出AC和OC,根据勾股定理列出方程,解方程即可.
解:(1)如图所示,作AB的垂直平分线,交OA于点C,则点C即为所求;
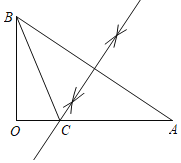
(2)由作图可得:BC=AC,
设BC=xcm,则AC=xcm,OC=(12﹣x)cm,
由勾股定理得,BC2=OB2+OC2,
即x2=82+(12﹣x)2,
解得x=![]() .
.
∴OC=12﹣![]() =
=![]()
答:线段OC的长是![]() cm.
cm.

练习册系列答案
相关题目