题目内容
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50, ![]() ≈1.41,
≈1.41, ![]() ≈2.24)
≈2.24)
【答案】解:
在Rt△ADB中,sin∠DAB= ![]() ,sin53.2°≈0.8,
,sin53.2°≈0.8,
所以AB= ![]()
![]() =20,
=20,
如图,过B作BD⊥AD于点D,过点B作BH⊥AC,交AC的延长线于H,
在Rt△AHB中,∠BAH=∠DAC﹣∠DAB=79.8°﹣53.2°=26.6°,
tan∠BAH= ![]() ,
,
∵tan26.6°≈0.50,
∴0.5= ![]() ,
,
AH=2BH,
BH2+AH2=AB2 , BH2+(2BH)2=202 , BH=4 ![]() ,所以AH=8
,所以AH=8 ![]() ,
,
∵货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,
∴BC=40× ![]() =10km,
=10km,
∴CH= ![]() =
= ![]() =2
=2 ![]() (km)
(km)
在Rt△BCH中,BH2+CH2=BC2 , CH=2 ![]() km,
km,
所以AC=AH﹣CH=8 ![]() ﹣2
﹣2 ![]() =6
=6 ![]() ≈13.4km,
≈13.4km,
答:此时货轮与A观测点之间的距离AC约为13.4km.
【解析】根据在Rt△ADB中,sin∠DAB= ![]() ,得出AB的长,进而得出tan∠BAH=
,得出AB的长,进而得出tan∠BAH= ![]() ,求出BH的长,即可得出AH以及CH的长,进而得出答案.
,求出BH的长,即可得出AH以及CH的长,进而得出答案.

【题目】初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
人数 | 1 | 2 | 8 | 11 | 5 |
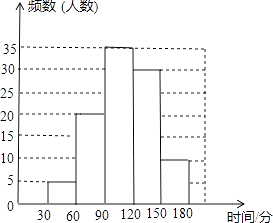
将这些数据按组距5(个字)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次打字成绩的众数是个,平均数是个.