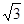题目内容
 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2011条棱分别停止在所到的正方体顶点处时,它们之间的距离是
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2011条棱分别停止在所到的正方体顶点处时,它们之间的距离是| 2 |
| 2 |
分析:根据题意找到规律:黑、白甲壳虫每爬行6条边后又重复原来的路径,可得当黑、白两个甲壳虫各爬行完第2011条棱分别停止时,黑甲壳虫停在点A1,白甲壳虫停在点B,则求BA1的长即可.
解答:解:∵黑甲壳虫爬行的路径为:AA1→A1D1→D1C1→C1C→CB→BA→AA1→A1D1→…,
白甲壳虫爬行的路径为:AB→BB1→B1C1→C1D1→D1A1→A1A→AB→BB1→…,
∴黑、白甲壳虫每爬行6条边后又重复原来的路径,
∵2011=335×6+1,
∴当黑、白两个甲壳虫各爬行完第2011条棱分别停止时,黑甲壳虫停在点A1,白甲壳虫停在点B,
∵正方体ABCD-A1B1C1D1的棱长为1,
根据勾股定理得:BA1=
.
故答案为:
.
白甲壳虫爬行的路径为:AB→BB1→B1C1→C1D1→D1A1→A1A→AB→BB1→…,
∴黑、白甲壳虫每爬行6条边后又重复原来的路径,
∵2011=335×6+1,
∴当黑、白两个甲壳虫各爬行完第2011条棱分别停止时,黑甲壳虫停在点A1,白甲壳虫停在点B,
∵正方体ABCD-A1B1C1D1的棱长为1,
根据勾股定理得:BA1=
| 2 |
故答案为:
| 2 |
点评:此题考查了立体图形的有关知识.注意找到规律:黑、白甲壳虫每爬行6条边后又重复原来的路径是解此题的关键.

练习册系列答案
相关题目
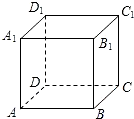 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2009条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2009条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )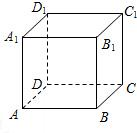 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是:AA1?A1D1?D1C1?C1C?CB?BA?AA1?A1D1…,
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是:AA1?A1D1?D1C1?C1C?CB?BA?AA1?A1D1…, 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2008条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从A点出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2008条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )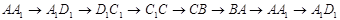 ……,白甲壳虫爬行的路线是:
……,白甲壳虫爬行的路线是: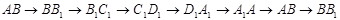 ……,那么当黑、白两个甲壳虫各爬行完第2008条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
……,那么当黑、白两个甲壳虫各爬行完第2008条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )
 D.
D.