题目内容
【题目】综合与探究
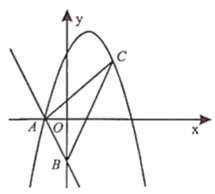
如图1,平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() .双曲线
.双曲线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
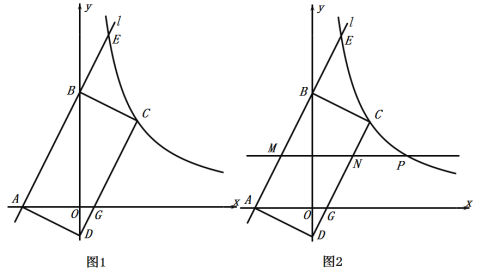
(1)求![]() 的值;
的值;
(2)在图1中以线段![]() 为边作矩形
为边作矩形![]() ,使顶点
,使顶点![]() 在第一象限、顶点
在第一象限、顶点![]() 在
在![]() 轴负半轴上.线段
轴负半轴上.线段![]() 交
交![]() 轴于点
轴于点![]() .直接写出点
.直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)如图2,在(2)题的条件下,已知点![]() 是双曲线
是双曲线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线分别交线段
轴的平行线分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
请从下列![]() ,
,![]() 两组题中任选一组题作答.我选择组题.
两组题中任选一组题作答.我选择组题.
A.①当四边形![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
B.①当四边形![]() 成为菱形时,求点
成为菱形时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)A.①
;(3)A.①![]() ,②
,②![]() ,
,![]()
![]() ,
,![]() ;B.①
;B.①![]() ,②
,②![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据点![]() 在
在![]() 的图象上,求得
的图象上,求得![]() 的值,从而求得
的值,从而求得![]() 的值;
的值;
(2)点![]() 在直线
在直线![]() 上易求得点
上易求得点![]() 的坐标,证得
的坐标,证得![]() 可求得点
可求得点![]() 的坐标,证得
的坐标,证得![]() 即可求得点
即可求得点![]() 的坐标;
的坐标;
(3)A.①作![]() 轴,利用平行四边的面积公式先求得点
轴,利用平行四边的面积公式先求得点![]() 的纵坐标,从而求得答案;
的纵坐标,从而求得答案;
②分类讨论,画出相关图形,构造全等三角形结合轴对称的概念即可求解;
B.①作![]() 轴,根据菱形的性质结合相似三角形的性质先求得点
轴,根据菱形的性质结合相似三角形的性质先求得点![]() 的纵坐标,从而求得答案;
的纵坐标,从而求得答案;
②分类讨论,画出相关图形,构造全等三角形结合轴对称的概念即可求解;
(1)![]() 在
在![]() 的图象上,
的图象上,
![]() ,
,
![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ;
;
(2)对于一次函数![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,![]() ,
,
在矩形![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
矩形ABCD中,AB∥DG,
∴![]()
![]()
![]()
![]()
∴点![]() 的坐标是
的坐标是![]() ,
,
故点![]() ,
,![]() ,
,![]() 的坐标分别是:
的坐标分别是:![]() ,
,![]() ,
,![]() ;
;
(3)A:①过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
![]()
![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
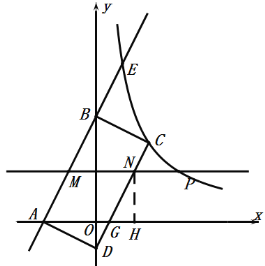
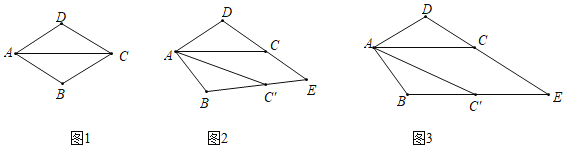
②当![]() 时,如图1,点
时,如图1,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;
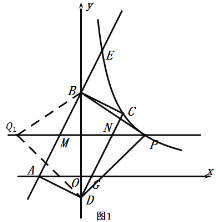
当![]() 时,如图2,过点
时,如图2,过点![]() 作
作![]() ⊥
⊥![]() 轴于
轴于![]() ,直线
,直线![]() 交
交 ![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
点![]() 的坐标是
的坐标是![]() ,
,
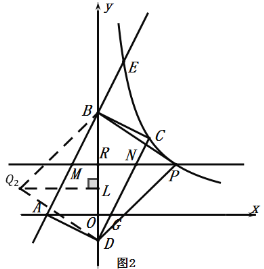
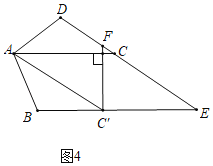
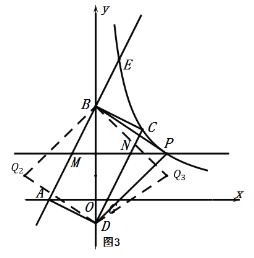
当![]() 时,如图3,点
时,如图3,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;
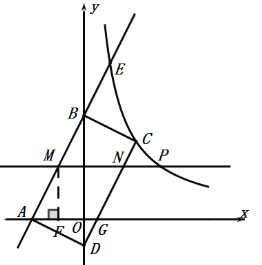
B:①过点![]() 作
作![]() 轴于点
轴于点![]()
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为菱形,
为菱形,![]() ,
,
∵![]() 轴,
轴,
∴ME∥BO,
∴![]() ,
,
![]() ,
,
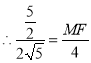 ,
,
![]() ,
,
![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ;
;
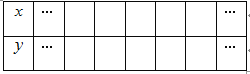
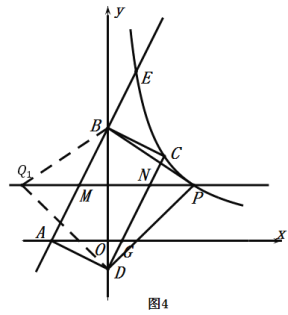
②当![]() 时,如图4,点
时,如图4,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;
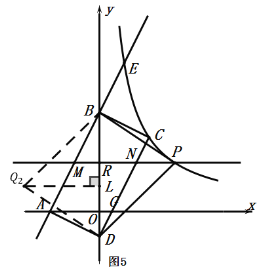
当![]() 时,如图5,过点
时,如图5,过点![]() 作
作![]() ⊥
⊥![]() 轴于
轴于![]() ,直线
,直线![]() 交
交 ![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
点![]() 的坐标是
的坐标是![]() ,
,
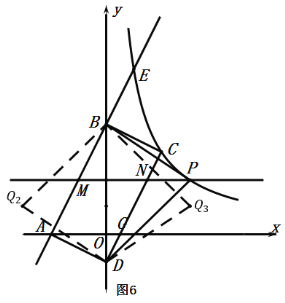
当![]() 时,如图6,点
时,如图6,点![]() 与点
与点![]() 关于
关于![]() 轴对称,由轴对称的性质可得:点
轴对称,由轴对称的性质可得:点![]() 的坐标是
的坐标是![]() ;
;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案