题目内容
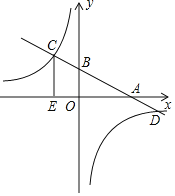
【题目】一次函数![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .顶点为
.顶点为![]() 的抛物线经过点
的抛物线经过点![]() .
.
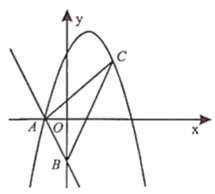
(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一动点.设点
为第一象限抛物线上一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 为何值时,
为何值时,![]() 的值最大,并求
的值最大,并求![]() 的最大值;
的最大值;
(3)在(2)的结论下,若点![]() 在
在![]() 轴上,
轴上,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;(3)
;(3)![]() 、
、![]() 、
、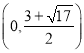 或
或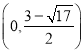
【解析】
(1)设抛物线的解析式为![]() ,代入点
,代入点![]() 的坐标即可求解;
的坐标即可求解;
(2)连接![]() ,可得点
,可得点![]() ,根据一次函数
,根据一次函数![]() 得出点
得出点![]() 、
、![]() 的坐标,然后利用三角形面积公式得出
的坐标,然后利用三角形面积公式得出![]() 的表达式,利用二次函数的表达式即可求解;
的表达式,利用二次函数的表达式即可求解;
(3)①当![]() 为直角边时,过点
为直角边时,过点![]() 和点
和点![]() 做垂线交
做垂线交![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,得出
,得出![]() ,再利用等腰直角三角形和坐标即可求解;②当
,再利用等腰直角三角形和坐标即可求解;②当![]() 为斜边时,设
为斜边时,设![]() 的中点为
的中点为![]() ,以
,以![]() 为圆心
为圆心![]() 为直径做圆于
为直径做圆于![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() 轴,先得出
轴,先得出![]() 和
和![]() 的值,再求出
的值,再求出![]() 的值即可求解.
的值即可求解.
解:(1)一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
![]() 抛物线的顶点为
抛物线的顶点为![]() ,
,
![]() 设抛物线解析式为
设抛物线解析式为![]() .
.
![]() 抛物线经过点
抛物线经过点![]() ,
,
![]() .
.
![]() .
.
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(2)解法一:连接![]() .
.
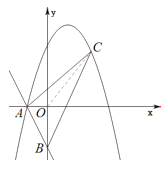
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
![]() .
.
一次函数![]() 与
与![]() 轴交于点
轴交于点![]() .则
.则![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
解法二:作![]() 轴,交
轴,交![]() 于点
于点![]() .
.
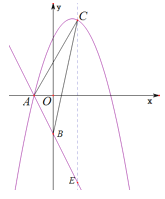
![]() 的坐标为
的坐标为![]() ,
,![]() .
.
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
解法三:作![]() 轴,交
轴,交![]() 于点
于点![]() .
.
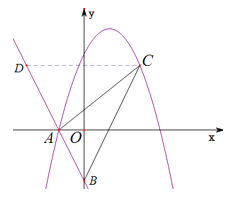
一次函数![]() 与
与![]() 轴交于点
轴交于点![]() .则
.则![]() ,
,
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
![]() .
.
把![]() 代入
代入![]() ,解得
,解得![]() ,
,
![]() .
.
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
解法四:构造矩形![]() .(或构造梯形
.(或构造梯形![]() )
)
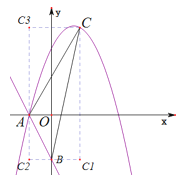
一次函数![]() 与
与![]() 轴交于点
轴交于点![]() .则
.则![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,![]() .
.
点![]() 为第一象限抛物线上一动点.点
为第一象限抛物线上一动点.点![]() 的横坐标为
的横坐标为![]() ,
,
设点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() .
.
当![]() 时,
时,![]() 的值最大,最大值为
的值最大,最大值为![]() ;
;
(3)由(2)易得点![]() 的坐标为
的坐标为![]() ,
,
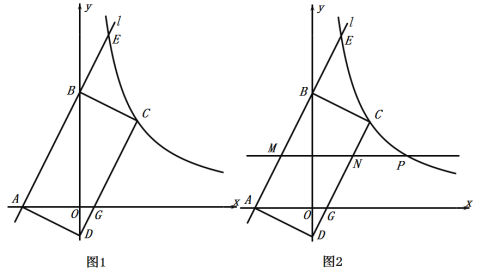
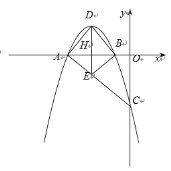
①当![]() 为直角边时,过点
为直角边时,过点![]() 和点
和点![]() 做垂线交
做垂线交![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,如下图所示:
,如下图所示:
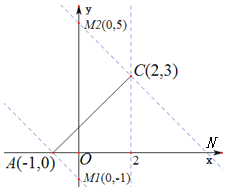
由点![]() 和点
和点![]() 的坐标可知:
的坐标可知:![]()
∴![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]()
由题可知:![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
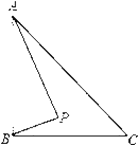
②当![]() 为斜边时,设
为斜边时,设![]() 的中点为
的中点为![]() ,以
,以![]() 为圆心
为圆心![]() 为直径做圆于
为直径做圆于![]() 轴于点
轴于点![]() 和点
和点![]() ,过点
,过点![]() 作
作![]() 轴,如下图所示:
轴,如下图所示:
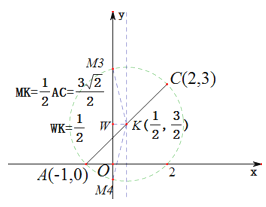
由点![]() 和点
和点![]() 的坐标可得点
的坐标可得点![]() 的坐标是
的坐标是![]()
∴![]() ,
,![]()
∴![]()
∴点![]() 的坐标为
的坐标为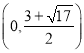 ,点
,点![]() 的坐标为
的坐标为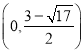
根据圆周角定理即可知道![]()
∴点![]() 和点
和点![]() 符合要求
符合要求
∴综上所述点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、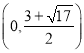 或
或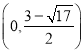 .
.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案